
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Неопределенный интеграл. 1. Множество первообразных функции имеет вид:
|
|
 1. Множество первообразных функции
1. Множество первообразных функции  имеет вид:
имеет вид:
А) 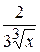 +С
+С  Б)
Б) 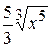 +С В)
+С В) 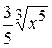 +С Г)
+С Г) 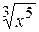 +С
+С
2. Множество первообразных функции  имеет вид:
имеет вид:
А) 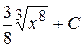 Б)
Б) 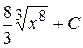 В)
В)  Г)
Г) 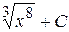
3. Множество первообразных функции  имеет вид:
имеет вид:
А) 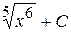 Б)
Б) 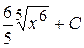 В)
В) 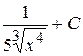 Г)
Г) 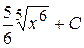
4. Множество первообразных функции 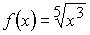 имеет вид:
имеет вид:
А) 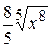 +С Б)
+С Б) 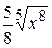 +С В)
+С В) 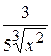 +С Г)
+С Г) 
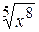 +С
+С
5. Множество первообразных функции 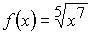 имеет вид:
имеет вид:
А) 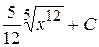 Б)
Б) 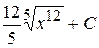 В)
В) 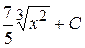 Г)
Г) 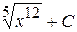
6. Множество первообразных функции 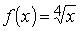 имеет вид:
имеет вид:
А) 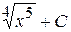 Б)
Б)  +С В)
+С В) 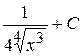
 Г)
Г) 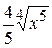 +С
+С
7. Множество первообразных функции 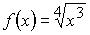 имеет вид:
имеет вид:
А)  Б)
Б)  + С В)
+ С В) 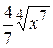 + С Г)
+ С Г) 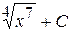
8. Множество первообразных функции  имеет вид:
имеет вид:
А) 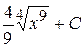 Б)
Б)  В)
В)  Г)
Г) 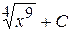
9. Множество первообразных функции  имеет вид:
имеет вид:
А) 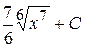 Б)
Б) 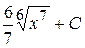 В)
В) 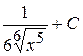 Г)
Г) 
10. Множество первообразных функции 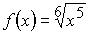 имеет вид:
имеет вид:
А)  Б)
Б) 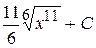 В)
В)  Г)
Г) 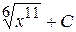
11. Множество первообразных функции 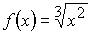 имеет вид:
имеет вид:
А) 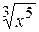 +С Б)
+С Б) 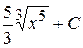 В)
В)  Г)
Г) 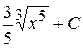
12. Множество первообразных функции 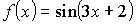 имеет вид:
имеет вид:
А) 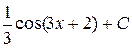 Б)
Б) 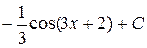
В) 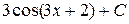 Г)
Г) 
13. Множество первообразных функции f(x) = 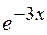 имеет вид:
имеет вид:
А) 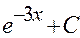 Б)
Б) 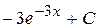 В)
В) 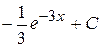 Г)
Г) 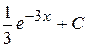
14. Множество первообразных функции f(x) = 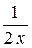 имеет вид:
имеет вид:
А) 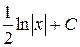 Б)
Б)  В)
В) 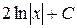 Г)
Г) 
15. Множество первообразных функции f(x) = 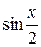 имеет вид:
имеет вид:
А)  Б)
Б) 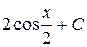 В)
В) 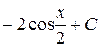 Г)
Г) 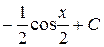
16. Множество первообразных функции f(x) =  имеет вид:
имеет вид:
А) 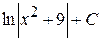 Б)
Б) 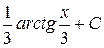 В)
В) 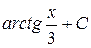 Г)
Г) 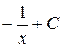
17. Множество первообразных функции f(x) =  имеет вид:
имеет вид:
А) 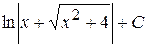 Б)
Б) 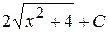
В) 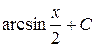 Г)
Г) 
18. Множество первообразных функции f(x) = 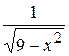 имеет вид:
имеет вид:
А)  Б)
Б) 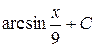
В) 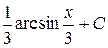 Г)
Г) 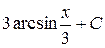
19. Множество первообразных функции f(x) = 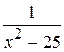 имеет вид:
имеет вид:
А) 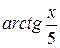 Б)
Б) 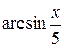
В) 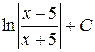 Г)
Г) 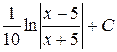
20. Множество первообразных функции f(x) = 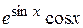 имеет вид:
имеет вид:
А) 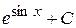 Б)
Б) 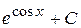 В)
В) 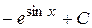 Г)
Г) 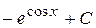
21. Множество первообразных функции f(x) = 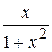 имеет вид:
имеет вид:
А) 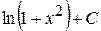 Б)
Б) 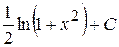
В) 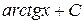 Г)
Г) 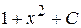
22. Множество первообразных функции f(x) = 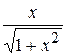 имеет вид:
имеет вид:
А) 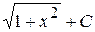 Б)
Б) 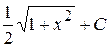
В) 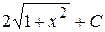 Г)
Г) 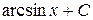
23. Множество первообразных функции f(x) = 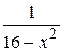 имеет вид:
имеет вид:
А) 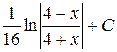 Б)
Б) 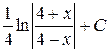
В)  Г)
Г) 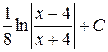
24. Множество первообразных функции f(x) =  имеет вид:
имеет вид:
А) 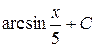 Б)
Б) 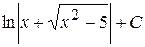
В) 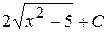 Г)
Г) 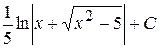
25. Вычислить неопределенный интеграл от функции f(x) = 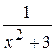 :
:
А) 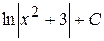 Б)
Б) 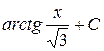
В) 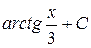 Г)
Г) 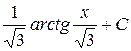
26. Вычислить неопределенный интеграл от функции f(x) = 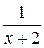 :
:
А) 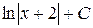 Б)
Б) 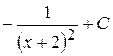
В) 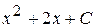 Г)
Г) 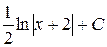
27. Множество первообразных функции f(x) = 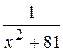 имеет вид:
имеет вид:
А) 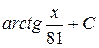 Б)
Б) 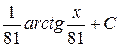
В) 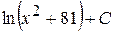 Г)
Г) 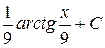

28. Множество первообразных функции f(x) = 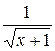 имеет вид:
имеет вид:
А) 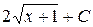 Б)
Б) 
В)  Г)
Г) 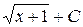
29. Множество первообразных функции f(x) = 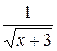 имеет вид:
имеет вид:
А)  Б)
Б) 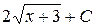
В) 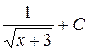 Г)
Г) 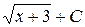
30. Множество первообразных функции f(x) = 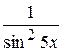 имеет вид:
имеет вид:
А) 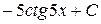 Б)
Б) 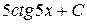
В) 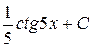 Г)
Г) 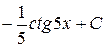
31. Множество первообразных функции f(x) = 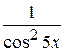 имеет вид:
имеет вид:
А) 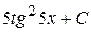 Б)
Б) 
В)  Г)
Г) 
32. Множество первообразных функции f(x) =  имеет вид:
имеет вид:
А) 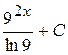 Б)
Б) 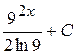 В)
В) 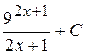 Г)
Г) 
33. Множество первообразных функции f(x) = 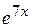 имеет вид:
имеет вид:
А) 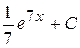 Б) 7
Б) 7 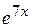 + С В)
+ С В) 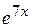 + С Г)
+ С Г) 
34. Множество первообразных функции f(x) = 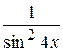 имеет вид:
имеет вид:
А) 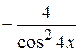 + С Б)
+ С Б) 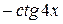 + С
+ С
В) 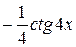 + С Г)
+ С Г) 
35. Множество первообразных функции f(x) =  имеет вид:
имеет вид:
А) 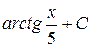 Б)
Б) 
В) 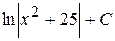 Г)
Г) 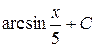
36. Функция F(x) называется первообразной функции f (x) на интервале (а, b), если для любого  выполняется равенство
выполняется равенство
А) 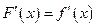
Б) 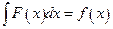
В) 
Г) 
37.Дифференциал от неопределенного интеграла равен 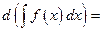
А) 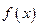
Б) 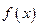 dx
dx
В) 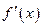
Г) 
38. Производная неопределенного интеграла равна 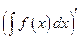
А) 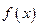
Б) 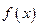 dx
dx
В) 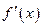
Г) 
39. Неопределенный интеграл от дифференциала некоторой функции равен 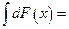
А) 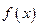
Б) 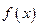 dx
dx
В) 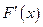
Г) 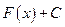
40. Пусть а- постоянная величина тогда 
А) 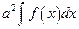
Б) 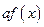
В) 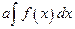
Г) 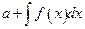
41. 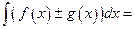
А) 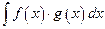
Б) 
В) 
Г) 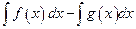
42. Формула интегрирования по частям имеет вид:
А) 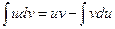
Б) 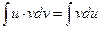
В) 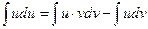
Г) 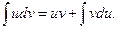
43. Пусть требуется вычислить интеграл 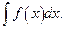 Сделаем подстановку
Сделаем подстановку 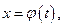 где
где  - функция, имеющая непрерывную производную. Тогда формула замены переменных в неопределенном интеграле имеет вид:
- функция, имеющая непрерывную производную. Тогда формула замены переменных в неопределенном интеграле имеет вид:
А) 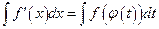
Б) 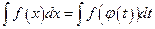
В) 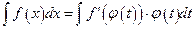
Г) 
44. Функция вида: 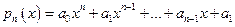 , где n – натуральное число,
, где n – натуральное число, 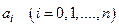 - постоянные коэффициенты, называется
- постоянные коэффициенты, называется
А) целой рациональной функцией;
Б) дробно-рациональной функцией
В) иррациональной функцией
Г) рациональной дробью
45. Корнем многочлена 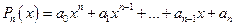 называется такое значение x0 переменной x, при котором
называется такое значение x0 переменной x, при котором
А) 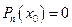
Б) 
В) 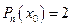
Г) 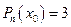
46. Если x 1, x 2, ….. x n- корни многочлена P n(x), а 0 – коэффициент многочлена при x n, то многочлен P n(x) можно представить в виде:
А) P n(x0) = 0
Б) P n(x) = а 0 (x – x 1)(x – x 2)…….(x - x n)
В) P n(x) = а 0 (x + x 1)(x + x 2)…….(x + x n)
Г) P n(x) = (x - x 1)(x - x 2)…….(x - x n)
47. Если x 1 – корень многочлена P n(x) кратности k1, x 2 – кратности k2, …, корень xr имеет кратность kr, при этом k1 + k2 +….+ kr = n, а 0 – коэффициент при x n разложение многочлена P n(x) можно записать в виде:
А) P n(x) = а 0 (x + x 1)(x + x 2)…….(x + x r)
Б) P n(x) = (x - x 1)(x - x 2)…….(x - x r)
В) P n(x) = а 0 (x – x 1) 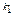 (x – x 2)
(x – x 2) 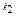 …….(x - x n)
…….(x - x n) 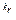
Г) P n(x) = а 0 (x + x 1) 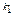 (x + x 2)
(x + x 2) 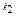 …….(x + x n)
…….(x + x n) 
48. Рациональная дробь называется правильной, если
А) степень числителя равна степени знаменателя
Б) степень числителя меньше степени знаменателя
В) степень числителя больше степени знаменателя
Г) степень числителя и степени знаменателя равны единице
49. 
А) 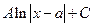
Б) 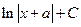
В) 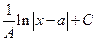
Г) 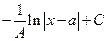
50. 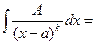
А) 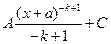
Б) 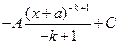
В) 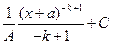
Г) 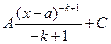
51. Непрерывная функция имеет
А) только одну первообразную
Б) бесконечное множество первообразных
В) две первообразных
52. Две различные первообразные одной и той же функции
А) равны между собой
Б) отличаются на константу
В) отличаются на некоторую функцию
53. К интегрируемым функциям относятся все
А) постоянные
Б) непрерывные
В) прерывные
54. Совокупность всех первообразных 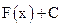 от функции f(x) называется
от функции f(x) называется
А) дифференциалом 
Б) определенным интегралом
В) неопределенным интегралом
55. Проверить соответствие формул:
1) 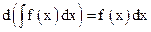 ; 2)
; 2)  ; 3)
; 3) 
А) верно
Б) ошибка в 2)
В) ошибка в 3)