Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Определенный интеграл
|
|
56. 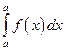 равен
равен
А) -1
Б) 1
В) 0
Г) а
57. для любого действительного числа С 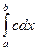 равен
равен
А) c (b-a)
Б) c (b+a)
В) - c (b-a)
Г) 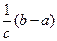
58. Если функция y = f (x) непрерывна на отрезке  и F (x) – какая либо ее первообразная на
и F (x) – какая либо ее первообразная на 
 , то формула Ньютона-Лейбница имеет вид:
, то формула Ньютона-Лейбница имеет вид:
А) 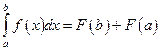
Б) 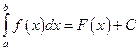
В) 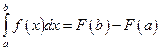
Г) 
59.Если с – постоянное число и функция f (x) итегрируема на  , то
, то
А) 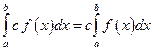
Б) 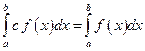
В) 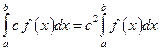
Г) 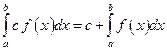
60. Если функция f (x) итегрируема на  и a < c < b, то
и a < c < b, то
А) 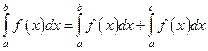
Б) 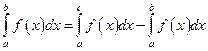
В) 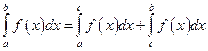
Г) 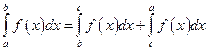
61. Если функция f (x) непрерывна на отрезке  , то существует точка
, то существует точка 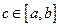 такая, что
такая, что
А) 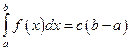
Б) 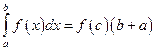
В) 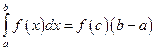
Г) 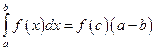
62. Если функции f1 (x) и f2 (x) непрерывные на отрезке  функции, и
функции, и 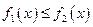 при
при 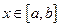 , то
, то
А) 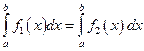
Б) 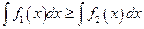
В) 
Г) 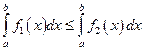
63. Если m и М – соответственно наименьшее и наибольшее значения функции y = f (x) на отрезке  , (a < b), то
, (a < b), то
А) 
Б) 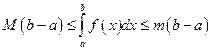
В) 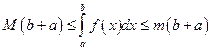
Г) 
64. Площадь фигуры, ограниченной кривыми y = f1 (x) и y = f2 (x), прямыми
x = a и x = b при условии 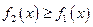 , можно найти по формуле
, можно найти по формуле
А) 
Б) 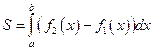
В) 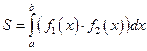
Г) 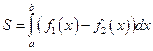
65. В выражении 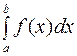 функция
функция  называется
называется
А) подынтегральным выражением
Б) интегральной суммой
В) подынтегральной функцией
66. Если непрерывные функции удовлетворяют неравенству 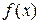 ≤
≤ 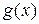 при
при 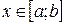 , то
, то
А) 
Б) 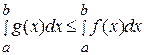
В) 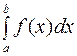 ≤
≤ 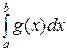
67. Функция 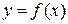 интегрируема на отрезке
интегрируема на отрезке 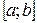 , если она на этом отрезке:
, если она на этом отрезке:
А) непрерывна
Б) монотонна
В) неотрицательна
68. В формуле интегрирования по частям для определенного интеграла 
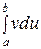 функции
функции 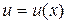 и
и 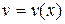 на отрезке
на отрезке 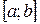 :
:
А) имеют непрерывные производные
Б) неположительны
В) постоянны
69. Если функция  интегрируема и неотрицательна на
интегрируема и неотрицательна на 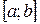 , где
, где  <
< 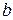 , то значение определенного интеграла будет
, то значение определенного интеграла будет
А) положительным
Б) неотрицательным
В) отрицательным
70. Площадь криволинейного сектора, т.е. плоской фигуры, ограниченной непрерывной линией 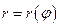 и двумя лучами
и двумя лучами 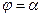 и
и 
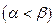 , где r и
, где r и 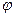 - полярные координаты, вычисляется по формуле:
- полярные координаты, вычисляется по формуле:
А) 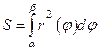
Б) 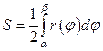
В) 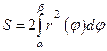
Г) 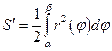
71. Пусть в прямоугольных координатах дана плоская кривая AB, уравнение которой y = f (x), где 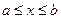 . Если функция y = f (x) и ее производная
. Если функция y = f (x) и ее производная 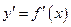 непрерывны на отрезке
непрерывны на отрезке  , то кривая AB имеет длину равную
, то кривая AB имеет длину равную
А) 
Б) 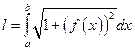
В) 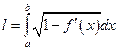
Г) 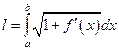
72. Если уравнение кривой AB задано в параметрической форме 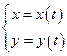 ,
, 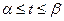 , где x (t) и y (t) – непрерывные функции с непрерывными производными и
, где x (t) и y (t) – непрерывные функции с непрерывными производными и 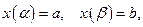 то длина
то длина 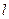 кривой AB находится по формуле
кривой AB находится по формуле
А) 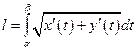
Б) 
В) 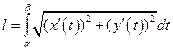
Г) 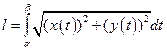
73. Вычислить определенный интеграл 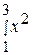 :
:
А) 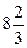 Б) 8 В) 4 Г) -
Б) 8 В) 4 Г) - 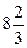
74. Вычислить определенный интеграл 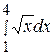 :
:
А) 1 Б) 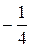 В)
В)  Г)
Г) 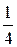
75. Вычислить определенный интеграл 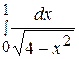 :
:
А) 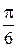 Б)
Б) 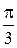 В)
В) 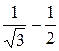 Г) 0
Г) 0
76. Вычислить определенный интеграл  :
:
А) -2 Б) -8 В) 0 Г) 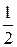
77. Вычислить определенный интеграл 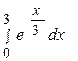 :
:
А) 3 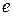 – 3 Б)
– 3 Б) 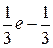 В)
В) 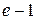 Г)
Г) 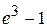
78. Вычислить определенный интеграл 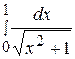 :
:
А) 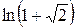 Б)
Б) 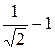
В)  Г)
Г) 
79. Вычислить определенный интеграл 
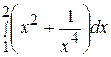 :
:
А) 2 Б) 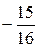 В)
В)  Г) 0
Г) 0
80. Вычислить определенный интеграл 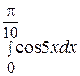 :
:
А) 1 Б) 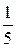 В) 0 Г) 5
В) 0 Г) 5
81. Вычислить определенный интеграл 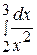 :
:
А) 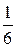 Б)
Б) 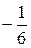 В) 2 Г)
В) 2 Г) 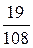
82. Вычислить определенный интеграл 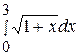 :
:
А) 1 Б) 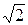 В)
В)  Г)
Г) 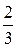
83. Вычислить определенный интеграл 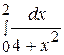 :
:
А)  Б)
Б) 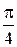 В)
В) 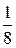 Г)
Г) 
84. Вычислить определенный интеграл 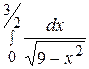 :
:
А) 0 Б) 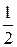 В)
В) 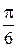 Г) 2
Г) 2 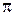
85. Вычислить определенный интеграл 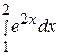 :
:
А) 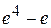 Б) 2
Б) 2 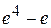 В)
В) 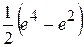 Г)
Г) 
86. Вычислить определенный интеграл 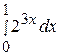 :
:
А) 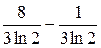 Б) 7 В) 21 Г)
Б) 7 В) 21 Г) 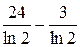
87. Вычислить определенный интеграл 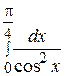 :
:
А) -1 Б) 2 В) 1 Г) 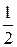
88. Вычислить площадь фигуры, ограниченной линиями:
у = 4 – х2 ; у = 0
А) 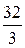 Б)
Б) 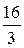 В) 10 Г) 16
В) 10 Г) 16
89. Вычислить площадь фигуры, ограниченной линиями:
у = lnx; х = e; у = 0
А) 1 Б) 2 В) 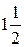 Г) 3
Г) 3
90. Вычислить площадь фигуры, ограниченной линиями:
у = х2; у = 2 – х2
А) 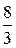 Б) 3 В) 4 Г)
Б) 3 В) 4 Г) 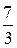
91. Вычислить площадь фигуры, ограниченной линиями:
у = х2 + 1; у = 0; х = -1; х = 3
А)  Б) 10 В) 15 Г)
Б) 10 В) 15 Г) 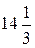
92. Вычислить площадь фигуры, ограниченной линиями:
у = 9 – х2; у = 0
А) 36 Б) 26 В) 10 Г) 32
93. Вычислить площадь фигуры, ограниченной линиями:
у = х2; у = 0; х = 4
А) 22 Б) 20 В) 13 Г) 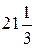
94. Вычислить площадь фигуры, ограниченной линиями:
у = х2; у = 0; х = – 3
А) 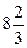 Б) 11 В) 9 Г)
Б) 11 В) 9 Г) 
95. Вычислить площадь фигуры, ограниченной линиями:
у = х3 + 2; у = 0; х = 0; х = 2
А) 4 Б) 8 В) 10 Г) 6
96. Вычислить площадь фигуры, ограниченной линиями:
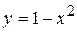 ;
; 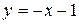
А) 4 Б) 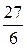 В) 6 Г)
В) 6 Г) 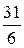
97. Вычислить площадь фигуры, ограниченной линиями:
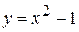 ;
; 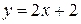
А) 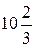 Б) 10 В)
Б) 10 В) 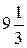 Г) 11
Г) 11
98. Вычислить площадь фигуры, ограниченной линиями:
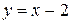 ;
; 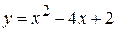
А) 4, 5 Б) 5 В) 4 Г) 
99. Вычислить определенный интеграл 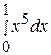 :
:
А) 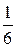 Б)
Б) 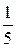 В) 1 Г) 0
В) 1 Г) 0
100. Вычислить определенный интеграл 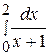 :
:
А) 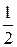 Б)
Б) 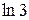 В) 1 Г)
В) 1 Г) 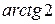
101. Вычислить определенный интеграл 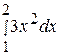 :
:
А) 7 Б) 6 В) 9 Г) 12
102. Вычислить определенный интеграл 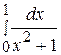 :
:
А) 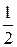 Б)
Б) 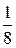 В)
В) 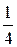 Г)
Г)