
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Введение. Теоретические основы обработки результатов измерений в физическом эксперименте - предмет отдельного курса лекций
|
|
Теоретические основы обработки результатов измерений в физическом эксперименте - предмет отдельного курса лекций. Ниже изложены основные понятия по обработке результатов прямых равноточных и косвенных измерений, как некоторый алгоритм действий, основанный на выводах теории погрешностей [1].
При любом измерении неизбежно возникают ошибки (погрешности измерений), приводящие к отклонению измеренного значения x от истинного значения 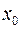 измеряемой величины X. Поэтому при записи результата измерений или вычислений принципиально важна оценка точности полученного числа. В физическом эксперименте результат представляется в виде:
измеряемой величины X. Поэтому при записи результата измерений или вычислений принципиально важна оценка точности полученного числа. В физическом эксперименте результат представляется в виде:
X = (54, 3  0, 2)
0, 2) 
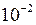 м
м 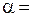 0, 7.
0, 7.
Такое представление означает, что истинное значение величины X с вероятностью 70% находится в диапазоне от 54, 1 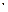
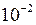 м до 54, 5
м до 54, 5 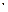
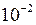 м на числовой оси.
м на числовой оси.
Цель настоящего пособия: научиться определять погрешность измерения. Иными словами, как, зная 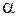 (доверительная вероятность), рассчитывать абсолютную погрешность или ошибку измерений Δ x (
(доверительная вероятность), рассчитывать абсолютную погрешность или ошибку измерений Δ x ( 0, 2
0, 2 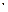
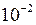 м), определяющую диапазон значений на числовой оси (доверительный интервал), в котором лежит ожидаемое истинное значение измеряемой величины.
м), определяющую диапазон значений на числовой оси (доверительный интервал), в котором лежит ожидаемое истинное значение измеряемой величины.
Вначале введём некоторые важные понятия и термины.
Абсолютная погрешность сама по себе ничего не говорит о точности измерения. Например, если абсолютная погрешность измерения напряжения Δ U = 20 мВ, то нельзя сказать, точным ли было измерение. Если напряжение равнялось 40 мВ, то очевидно измерение грубое. Если же напряжение было равно 220 В, то измерение можно считать точным. Чтобы охарактеризовать точность измерения, вводят относительную погрешность:
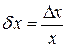 .
.
Если, 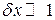 то измерение точное. Если это условие не выполняется, то измерение надо считать неточным.
то измерение точное. Если это условие не выполняется, то измерение надо считать неточным.
Для введения основных понятий и в качестве иллюстрации рассмот-рим простейшую лабораторную работу: «Определение ускорения сво-бодного падения при помощи математического маятника». Из известной формулы периода колебаний математического маятника получаем выражение для вычисления ускорения свободного падения:

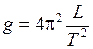 .
. 

 (1)
(1)
Цель работы: измеряя длину нити маятника L и время одного полного колебания T, по формуле (1) определить ускорение свободного падения g. Измерения L и Т, сделанные при помощи приборов, называются прямыми измерениями. Ускорение свободного падения g рассчитывается по формуле (1). Такое измерение называется косвенным измерением.
Формула, по которой после подстановки результатов прямых измерений получают результат косвенного измерения, называется рабочей формулой. В нашем примере это формула (1). Она даёт связь между результатом косвенного измерения g и результатами прямых измерений L и T. Рабочая формула является исходной при выводе формулы для расчета погрешности косвенного измерения (см. ниже).
В нашей модельной работе, если делать измерения времени не для одного, а для N полных колебаний маятника, рабочая формула имела бы другой вид:
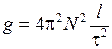 ,
,  (2)
(2)
где 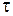 - время N полных колебаний маятника.
- время N полных колебаний маятника.
Ещё одно понятие - равноточные измерения. Равноточными называются измерения, выполненные в одинаковых условиях: неизменными должны оставаться объекты исследования, используемые приборы, условия и время проведения эксперимента.