
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Учет случайных погрешностей
|
|
Важно понять, что в тех случаях, когда основную роль играет случайная погрешность, все оценки точности измерений можно сделать только с некоторой вероятностью. Для нахождения случайной погрешности измерение нужно повторить несколько раз.
Пусть сделано n измерений некоторой величины 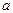 . Получены значения
. Получены значения 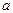 1,
1, 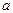 2,...,
2,..., 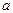 n. Из-за случайных погрешностей эти значения в общем случае отличаются друг от друга и от истинного значения
n. Из-за случайных погрешностей эти значения в общем случае отличаются друг от друга и от истинного значения 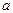 . Задача состоит в том, чтобы по этим данным найти наиболее вероятное значение искомой величины
. Задача состоит в том, чтобы по этим данным найти наиболее вероятное значение искомой величины 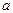 вер и абсолютную случайную погрешность D
вер и абсолютную случайную погрешность D 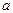 сл.
сл.
Метод расчета основан на теории вероятностей. Наиболее вероятное значение искомой величины находят как среднее арифметическое из результатов всех измерений, это значение принимают за истинное:
 (1)
(1)
Погрешность D 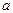 сл вычисляют через среднюю квадратичную погрешность
сл вычисляют через среднюю квадратичную погрешность
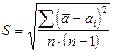 (2)
(2)
и так называемый коэффициент Стьюдента t
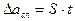 (3)
(3)
Коэффициент Стьюдента находят по таблице 1 в зависимости от числа измерений n и требуемой надежности результата α.
Если погрешности обусловлены только случайными причинами, то, найдя 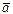 и
и  , результат записывают в виде
, результат записывают в виде
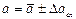 , при a=...
, при a=...
Такая запись означает, что истинное значение 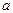 находится в интервале от (
находится в интервале от (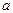 -D
-D 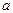 сл,) до (
сл,) до (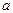 +D
+D 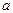 сл) с вероятностью a. Величину a иначе называют коэффициентом надежности. Этот интервал называют доверительным интервалом. Например, если h = (13, 52 ± 0.11) мм с вероятностью a=0, 70, то в 70% случаев истинное значение будет лежать в интервале от 13, 63 мм до 13, 41 мм, а в 30% случаев вне этого интервала.
сл) с вероятностью a. Величину a иначе называют коэффициентом надежности. Этот интервал называют доверительным интервалом. Например, если h = (13, 52 ± 0.11) мм с вероятностью a=0, 70, то в 70% случаев истинное значение будет лежать в интервале от 13, 63 мм до 13, 41 мм, а в 30% случаев вне этого интервала.
Таблица 1. Коэффициенты Стьюдента
 a
n a
n
| 0, 70 | 0, 80 | 0, 90 | 0, 95 | 0, 99 |
| 1, 3 | 1, 9 | 2, 9 | 4, 3 | 9, 9 | |
| 1, 2 | 1, 5 | 2, 1 | 2, 8 | 4, 6 | |
| 1, 1 | 1, 4 | 1, 9 | 2, 4 | 3, 7 | |
| 1, 1 | 1, 4 | 1, 9 | 2, 3 | 3, 4 | |
| µ | 1, 0 | 1, 3 | 1, 6 | 2, 0 | 2, 9 |