Статистический вывод

Статистика имеет дело с большим числом предметов и явлений, которые образуют генеральную совокупность. Однако исследователь обычно имеет дело с ограниченной частью генеральной совокупности, называемой выборочной совокупностью, или просто выборкой, по изучению которой он делает определенные выводы о генеральной совокупности[123].

Каковы же математические основания этих выводов?

Если F (х) — интегральная функция распределения генеральной совокупности, определяющая вероятность того, что х< Х, и если (х) — эмпирическая функция распределения выборки, то по теореме Бернулли при бесконечном увеличении объема выборки эмпирическое распределение по вероятности стремится к распределению теоретическому:

.

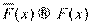Характеристики распределения генеральной совокупности принято называть параметрами 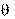, а характеристики выборочного распределения — оценками параметров .

Статистическую выборку можно производить многократно, используя множество способов, и всякий раз будут получаться новые значения оценок параметров.

Следовательно, каждый параметр имеет выборочное распределение оценок. В этой связи вводится понятие точности оценки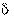

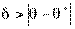
и надежности (или доверительной вероятности) у как вероятности того, что 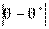< 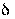, а именно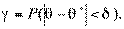

При исследовании генеральной совокупности, подчиняющейся нормальному закону, находят оценки параметров а и ; в случае распределения Пуассона — оценку параметра m.

Результат, полученный в выборке (обычно это среднеарифметическое или дисперсия), еще мало о чем говорит. Необходимо определить точность () и надежность (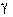) этой оценки. Без этого результат выборки не имеет смысла, поскольку оценка пара- метра является случайной величиной.

Точность оценки рассчитывается при определенных предположениях о распределении в генеральной совокупности. Может случиться, что генеральная совокупность отклоняется от предполагаемого теоретического распределения и, следовательно, расхождение эмпирического и теоретического распределения обусловлено не случайностью выборки, а тем, что данная генеральная совокупность характеризуется другим теоретическим распределением.

Всякое предположение о распределении генеральной совокупности называется статистической гипотезой. Встает проблема проверки статистической гипотезы. Гипотеза может касаться общего вопроса соответствия выборочного эмпирического и теоретического распределения. Она может относиться и к сопоставлению тех или иных параметров, например средних или дисперсий.

Обычно, следуя идее Дж.Неймана и Э.Пирсона, принимается начальная, или нулевая, гипотеза об отсутствии различия, которая обозначается 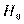[124].

В каждом отдельном случае определяется характеристика (критерий), по которой идет проверка. Если проверяется какой- либо параметр, а выборочное распределение его при данной гипотезе хорошо известно, то устанавливается предел вероятности, или уровень значимости. Значения характеристики, вероятности которых меньше уровня значимости, образуют так называемую критическую область, а значения, вероятности которых больше уровня значимости — область допустимых значений. Пусть дано выборочное распределение некоторой характеристики и (рис. 7).

Возможны два типа ошибок — так называемые ошибки первого и второго рода. Ошибка первого рода состоит в отбрасыва-

нии нулевой гипотезы 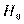, когда она верна. Ошибка второго рода связана с принятием нулевой гипотезы, когда она неверна.

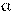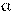Уровень значимости определяет вероятность ошибки первого рода. Обозначим вероятность ошибки второго рода . С уменьшением увеличивается . Величина 1 — называется мощностью критерия, с увеличением которой уменьшается вероятность ошибки второго рода[125].

При проверке гипотез приходится находить разумное соотношение уровня значимости и мощности критерия. Нельзя сделать

как угодно малыми одновременно 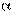и , и 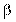. Здесь следует учитывать сложившуюся ситуацию. Это можно представить графически (рис. 8).

Кривая А связана с гипотезой 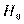. Кривая В связана с альтернативной гипотезой 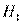; 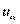— значение критерия, соответствующее уровню значимости .

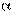Площадь справа от 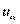под кривой 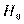дает 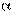— вероятность ошибки первого рода.

Значение 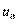соответствует генеральной характеристике. Точка 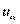определяет критическую область в том смысле, что вероятность значений 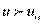оказывается меньше уровня значимости 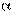(заштрихованная площадь справа от 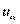равна 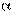); 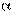обычно полагают равным 1, 2 и 5%. Для каждого критерия строятся специальные таблицы, в которых имеются значения для каждой вели- чины значения 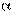и объема выборки.

Если уменьшать 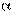, то, следовательно, будет уменьшаться вероятность отбрасывания верной гипотезы, иначе говоря, станет меньше вероятность ошибки первого рода, но вместе с тем расширится область допустимых значений критерия. Таким образом, если в действительности нулевая гипотеза неверна, то увеличивается вероятность принятия неверной гипотезы.

Когда нулевая гипотеза неверна, то тем самым верна какая-то другая, альтернативная гипотеза 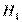. Возможны такие случаи:

1) критерий отвергает 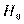, и верна ;

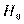2) критерий отвергает 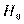, а верна ;

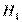3) критерий допускает 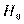, и верна ;

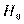4) критерий допускает 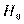, а верна .

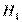Во втором и третьем случаях проверка гипотезы приводит к правильному выводу. Первый случай обусловливает ошибку первого рода, четвертый случай — второго рода.

Площадь слева от 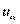под кривой 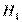определяет 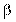, вероятность ошибки второго рода, т.е. вероятность принять гипотезу, когда она неверна.

Таковы некоторые положения о статистическом выводе. Использование математического аппарата статистического вывода имеет исключительно большое значение для социологии, так как, во-первых, социолог практически может проанализировать всю генеральную совокупность, а во-вторых, элементы генеральной совокупности в социологии гораздо более сложны и специфичны, чем в других областях науки.

Если ставится задача установить по выборке закон распределения, то используется так называемый критерий . При сравнении двух выборочных средних используется t-критерий, при сравнении двух выборочных дисперсий — F-критерий[126].