
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Измерение связи
|
|
Из школьного курса математики известно понятие функциональной связи, когда каждому значению независимой перемен- ной (аргумента х) ставится определенное значение зависимой переменной (функции у):
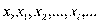
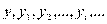
Функция может быть однозначной и многозначной. Так, дли- на окружности есть однозначная функция радиуса: 1=2 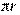 . Квад-
. Квад-
ратный корень из действительного числа — двузначная функция этого числа: у= 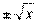 . Обратные тригонометрические функции угла дают простейший пример многозначных функций.
. Обратные тригонометрические функции угла дают простейший пример многозначных функций.
На графике, в случае однозначной функции, каждой паре значений х и у соответствует точка плоскости. Множество этих точек на плоскости представляет собой графическое изображение функциональной связи, или график функции у=1(х).
Однако в природе существуют не только функциональные связи такого рода.
Рассмотрим обычную игру в карты. При сдаче игрок получает некоторое множество карт. При следующей — другое множество карт и т.д. При каждой сдаче получается новая комбинация. Налицо — связь между сдачей и комбинацией карт игрока.
В этом случае с изменением одной переменной происходит изменение распределения другой переменной. Связь этих переменных называется статистической. Если оказывается, что с изменением одной переменной изменяется среднее значение другой, то говорят, что между этими переменными существует корреляционная связь.
Например, требуется определить зависимость между ростом жены и мужа. Для примера рассмотрим 100 супружеских пар. На плоскости дана прямоугольная система координат, по оси х откладывается рост мужа, по оси у — рост жены. Точкой на плоскости отмечается каждая супружеская пара. Полученное графическое изображение называется корреляционным полем (рис. 9).

В нашем случае должно быть 100 точек, которые как-то заполняют плоскость этого корреляционного поля. Для каждого класс-интервала х отбираем все соответствующие ему точки. Находим их среднее значение 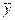 . Эту точку наносим на график, обозначая ее крестиком, чтобы выделить среди прочих. Соединяем ломаной все отмеченные крестиком точки. Полученная линия показывает изменение среднего значения роста жены с изменением
. Эту точку наносим на график, обозначая ее крестиком, чтобы выделить среди прочих. Соединяем ломаной все отмеченные крестиком точки. Полученная линия показывает изменение среднего значения роста жены с изменением
роста мужа от одного класс-интервала к другому. Эта линия называется эмпирической линией регрессии.
Если рассмотреть 100 других пар, то получится несколько иная эмпирическая линия регрессии. Если уменьшить величину класс-интервала, то линия покажет увеличение числа звеньев, сохранив в целом контур. Можно убедиться, что все эмпирические линии регрессии каких-либо двух переменных всегда лежат около некоторой плавной линии, называемой теоретической линией регрессии, или просто линией регрессии[127]. Ее уравнение называется уравнением регрессии. Если мы рассматриваем изменение среднего у от х, то получится уравнение регрессии у на х:
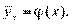
Если рассматриваем изменение среднего  от
от 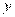 , то уравнение регрессии
, то уравнение регрессии 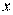 на
на 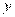 ;
;
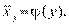
При 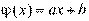 говорят о линейной регрессии
говорят о линейной регрессии 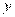 на
на 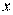 , т.е.
, т.е. 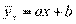 . Аналогично можно ввести уравнение регрессии х на у:
. Аналогично можно ввести уравнение регрессии х на у:
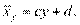
Как найти коэффициенты уравнений регрессии? Предположим, что дано и объектов, характеризующихся двумя переменными: 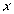 и
и 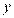 . Для простоты полагаем, что средние
. Для простоты полагаем, что средние 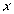 и
и 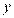 равны 0. Выбираем прямоугольную систему координат
равны 0. Выбираем прямоугольную систему координат 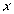
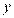 , строим корреляционное поле, устанавливаем класс-интервалы для
, строим корреляционное поле, устанавливаем класс-интервалы для 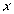 и для
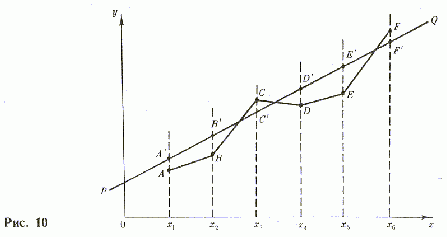
и для 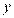 , проводим эмпирические линии регрессии, полагая, что искомые линии регрессии — прямые (рис. 10). Символически данная зависимость обозначается так:
, проводим эмпирические линии регрессии, полагая, что искомые линии регрессии — прямые (рис. 10). Символически данная зависимость обозначается так: 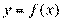 .
.
Линия ACDF — эмпирическая линия регрессии 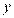 на
на 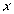 ; PQ— линия регрессии, а ее уравнение
; PQ— линия регрессии, а ее уравнение 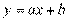 , коэффициенты котороro
, коэффициенты котороro 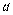 и
и 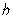 неизвестны и их надо найти.
неизвестны и их надо найти.
Коэффициенты теоретической линии регрессии находят по методу наименьших квадратов: ищут эту линию при том условии, чтобы сумма квадратов расстояний эмпирической линии регрессии от теоретической была бы минимальной. Иначе говоря, теоретическая линия регрессии должна иметь наиближайшее расположение ко всем точкам эмпирической линии регрессии.
Если мы обозначили ординату теоретической линии регрессии 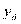 , эмпирической —
, эмпирической — 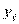 , то надо найти минимум величины:
, то надо найти минимум величины:
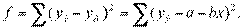
Это означает, что
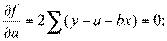
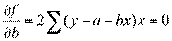 .
.
Получаем нормальные уравнения для определения коэффициентов линии регрессии:
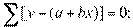
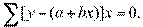
или
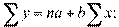
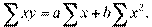
Поскольку средние 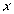 и
и 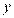 , как мы предположили, равны нулю
, как мы предположили, равны нулю
то 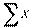 = 0;
= 0; 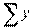 = 0 и, следовательно,
= 0 и, следовательно, 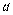 = 0;
= 0; 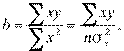
где 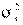 — дисперсия
— дисперсия 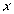 .
.
Найденный коэффициент 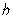 называется коэффициентом регрессии
называется коэффициентом регрессии 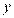 на
на 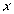 и обозначается
и обозначается 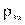 .
.
Аналогично можно построить линию регрессии 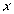 на
на 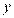 и соответственно найти коэффициент:
и соответственно найти коэффициент:
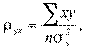
где  — дисперсия y.
— дисперсия y.
Коэффициент корреляции определяют как среднее геометрическое из коэффициентов регрессии[128]:
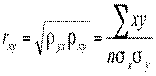
Дадим геометрическую интерпретацию коэффициенту корреляции[129] (рис. 11).
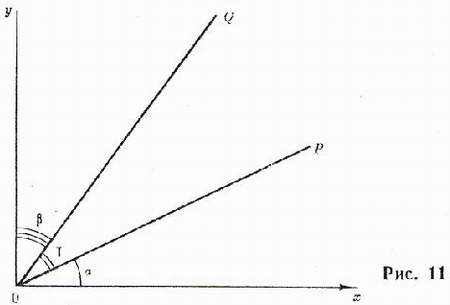
OP — это линия регрессии у на х;
OQ — линия регрессии х на у; 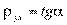 ;
; 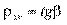 по определению коэффициентов регрессии
по определению коэффициентов регрессии
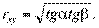
Если корреляции нет, то или линия OP, или OQ или обе вместе совпадают с осями координат, так как: 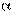 =0 или
=0 или 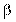 =0 и, следовательно, r = 0.
=0 и, следовательно, r = 0.
Еcли корреляционная связь переходит в функциональную, то обе линии регрессии совпадают. Тогда 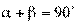 ,
, 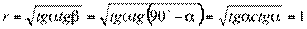 , т.е. коэффициент корреляции равен 1.
, т.е. коэффициент корреляции равен 1.
Чем теснее связь между переменными, тем меньше угол меж- ду обеими линиями регрессии.
Рассмотренный коэффициент корреляции измеряет линейную связь между двумя количественными переменными. Этим, одна-
ко, не исчерпывается все возможное многообразие связей в социологии.
Во-первых, переменные могут иметь криволинейную регрессию: линия регрессии может быть параболой, кубической параболой, экспонентой и т.п. В каждом случае надо находить пути измерения связи между данными переменными.
Во-вторых, возможно наличие связи между более чем двумя переменными. Это проблема множественной корреляции, или многофакторного корреляционного анализа.
В-третьих, возможно существование связи между не только количественными переменными. В этом случае в статистике и социологии используются специальные показатели связи.
В случае криволинейной регрессии вместо коэффициента корреляции (иногда говорят «коэффициента линейной, или парной, корреляции») вводится корреляционное отношение[130].

где 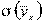 — среднее квадратичное отклонение условных средних
— среднее квадратичное отклонение условных средних 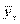 от их средней,
от их средней, 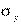 — среднее квадратичное отклонение
— среднее квадратичное отклонение 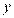 (аналогично для
(аналогично для 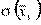 и
и 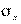 ) и корреляционное отношение
) и корреляционное отношение

Следовательно, прежде чем определять связь между количественными переменными социального объекта, необходимо сначала построить их линии регрессии и оценить характер регрессии. В том случае, если эмпирическая линия регрессии находится близко от некоторой прямой, можно вычислить коэффициент линейной корреляции Пирсона. Если же эмпирическая линия регрессии — явный изгиб, то надо использовать корреляционное отношение. При наличии более двух количественных переменных применяют частные коэффициенты корреляции[131].
Если, например, рассматривают три переменные х, у, z, то вводят частные коэффициенты корреляции 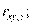
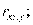
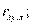
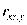 определяет связь между х и r при исключении влияния переменной у:
определяет связь между х и r при исключении влияния переменной у:
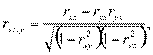
где справа находятся обычные коэффициенты парной корреляции. Выражения для двух других коэффициентов получаются простой круговой перестановкой индексов в правой части.
Можно также ввести понятия частых коэффициентов корреляции и сводный коэффициент для и переменных.
Для измерения связи между качественными (номинальными) переменными используется таблица сопряженности.
| B1 | B2 | … | Bj | … | |
| A1 | n11 | n12 | … | n1j | n1. |
| A2 | n21 | n22 | … | n2j | n2. |
| … | … | … | … | … | … |
| Ai | ni1 | ni2 | … | nij | ni. |
| … | n. 1 | n. 2 | … | n. j | n |
Имеются два номинальных признака (переменные) А и В, которые принимают соответственно значения 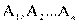 и
и 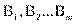 . Это могут быть, например, образование (начальное, неполное среднее, среднее и высшее), социальное положение (рабочий, крестьянин, служащий, военный), возрастная группа (ученики, молодые рабочие, средний возраст, пожилые кадровые рабочие), участие в общественной жизни (не участвуют, слабо участвуют, участвуют, активно участвуют) и др.
. Это могут быть, например, образование (начальное, неполное среднее, среднее и высшее), социальное положение (рабочий, крестьянин, служащий, военный), возрастная группа (ученики, молодые рабочие, средний возраст, пожилые кадровые рабочие), участие в общественной жизни (не участвуют, слабо участвуют, участвуют, активно участвуют) и др.
Рассмотрим N лиц и их распределение по признакам А и В.
В каждой клетке первой строки пишется число лиц, которые одновременно обладают значением А, признака А и соответствующими значениями признака В, т.е. в левой клетке первой строки стоит и,, число лиц, обладающих признаками А, и В, одновременно, во второй клетке — 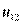 число лиц, обладающих признаками
число лиц, обладающих признаками 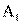 и
и 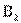 и т.д. Вообще в клетке на пересечении i-й строки и j-го столбца находится число
и т.д. Вообще в клетке на пересечении i-й строки и j-го столбца находится число 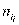 , обозначающее число лиц, обладающих признаками
, обозначающее число лиц, обладающих признаками 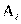 и
и 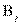 .
.
Таблица сопряженности в данном случае очень сходна с корреляционной таблицей с той лишь разницей, что первая дает со-
вместные частоты качественных значений признаков, а вторая — совместные частоты класс-интервалов количественных признаков.
Вместо 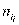 введем относительную частоту
введем относительную частоту 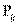 .
.
Пирсон предложил следующий коэффициент связи признаков А и В:
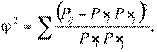
который сконструирован так, что квадраты отклонений взвешенны по отношению к ожидаемым частотам и нейтрализованно влияние значков (как, в случае диоперсии).
При полной независимости переменных 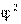 = 0, при полной зависимости число строк равняется t — числу столбцов, и в таком случае
= 0, при полной зависимости число строк равняется t — числу столбцов, и в таком случае 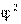 = t — 1.
= t — 1.
Иногда используют так называемый коэффициент сопряженности в виде
где 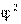 — только что рассмотренный коэффициент. Коэффициент С
— только что рассмотренный коэффициент. Коэффициент С
дает более прямое непосредственное указание на связь между признаками.
Для определения связи между ранжированными переменными можно использовать так называемый ранговый коэффициент Спирмена:
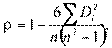
где n — число объектов; 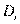 — разности между значениями переменных для i-го объекта.
— разности между значениями переменных для i-го объекта.
Рассмотрим числовой пример: даны 13 лиц, проранжированных по двум признакам. Результаты таковы:
| Лица | Ранги | Разности | Лица | Ранги | Разности | ||||
| I | II | Di | 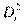
| I | II | Di | 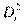
| ||
| А | Ж | -2 | |||||||
| Б | З | -5 | |||||||
| В | И | ||||||||
| Г | 4, 5 | 3, 5 | 12, 25 | К | 4, 5 | 6, 5 | 42, 25 | ||
| Д | -1 | 8, 5 | -1, 5 | 2, 25 | |||||
| Е | -2 | 8, 2 | -2, 5 | 6, 25 |
И первом столбце — лица; во втором — их ранги по первой переменной (признаку); в третьем — их ранги по второй переменной (признаку); в четвертом — разность рангов этих лиц. В последнем столбце — квадраты разностей, которые используются в формуле.
Можно произвести вычисления. Получим
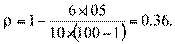
Большое значение для социологических исследований имеет бисериальный коэффициент корреляции, определяющий связь между, количественной переменной и дихотомической качественной переменной. Он вычисляется по формуле
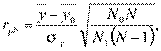
где 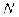 , — число индивидов с положительным ответом по признак;
, — число индивидов с положительным ответом по признак; 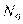 — число индивидов с отрицательным ответом по признаку;
— число индивидов с отрицательным ответом по признаку;
N — общее число индивидов; 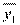 — средняя в
— средняя в 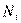 ;
; 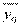 — средняя в
— средняя в 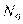 ; у — средняя всей группы;
; у — средняя всей группы;
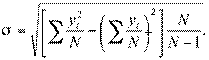
Пример[132].
| Лица | Количественные переменные | Качественная переменная | Лица | Количественные переменные | Качественная переменная | ||
| + | – | + | – | ||||
| А | Ж | ||||||
| Б | З | ||||||
| В | И | ||||||
| Г | К | ||||||
| Д | Л | ||||||
| Е | М |
Вычисления дают: 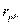 =0, 57.
=0, 57.
Представляет интерес для социологии группа коэффициентов для измерения корреляции в четырехклеточной таблице, которые измеряют связь между дихотомическими переменными.
Для таблицы в виде
| – | + | ||
| + | A | B | A + B |
| – | C | D | C + D |
| A + C | B + D |
имеют место коэффициенты
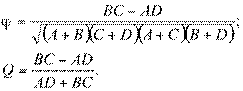
При измерении связи в конкретном социологическом исследовании мы вычисляем коэффициент корреляции по выборке. По сути дела, мы всегда располагаем только некоторой оценкой коэффициента корреляции генеральной совокупности. Любая выборочная оценка, как мы уже отмечали, требует проверки. Без указания точности расчета и проверки статистической гипотезы выборочная оценка не имеет смысла, к ней неизвестно как подступиться.
Остановимся на статистических оценках коэффициента парной корреляции r и рангового коэффициента корреляции Спирмена ρ.
Критические величины коэффициента корреляции Спирмена ρ
| № | Уровень существенности | № | Уровень существенности | ||
| 0, 05 | 0, 01 | 0, 05 | 0, 01 | ||
| 1, 000 | 0, 506 | 0, 712 | |||
| 0, 900 | 1, 000 | 0, 456 | 0, 645 | ||
| 0, 829 | 0, 943 | 0, 425 | 0, 601 | ||
| 0, 714 | 0, 893 | 0, 399 | 0, 564 | ||
| 0, 643 | 0, 833 | 0, 377 | 0, 534 | ||
| 0, 600 | 0, 783 | 0, 359 | 0, 508 | ||
| 0, 564 | 0, 746 | 0, 343 | 0, 485 | ||
| 0, 329 | 0, 465 | ||||
| 0, 317 | 0, 448 | ||||
| 0, 306 | 0, 432 |
В случае нормального распределения для r дается выражение ошибки:

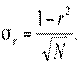
Это означает, что коэффициент корреляции 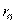 генеральной совокупности с вероятностью 0, 997 находится в интервале
генеральной совокупности с вероятностью 0, 997 находится в интервале
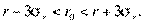
Если использовать специальные таблицы, то можно построить доверительный интервал при данной доверительной вероятности и проверить нулевую гипотезу равенства выборочного и генерального коэффициентов корреляции.
Для проверки ρ Спирмена используют таблицу критических величин. Если 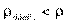 при данном количестве объектов и данном уровне существенности, то считается, что связь между ранговыми переменными существует. В нашем примере, вычисляя коэффициент Спирмена, мы получим значение
при данном количестве объектов и данном уровне существенности, то считается, что связь между ранговыми переменными существует. В нашем примере, вычисляя коэффициент Спирмена, мы получим значение 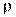 =0, 36. Используя таблицу, мы получим для n = 10 и уровня существенности 0, 05
=0, 36. Используя таблицу, мы получим для n = 10 и уровня существенности 0, 05 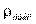 =0, 564. Следовательно,
=0, 564. Следовательно, 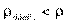 , и мы полагаем, что ранжирование коррелировано.
, и мы полагаем, что ранжирование коррелировано.
Глава третья
Психологические тесты и социологические шкалы