
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Примеры решения задач. Задача 1. Сила тока в проводнике изменяется за время от t1 = 3 c до t2 = 7 с по закону I = At2 + B, где А = 0,1 А/с2
|
|
Задача 1. Сила тока в проводнике изменяется за время от t1 = 3 c до t2 = 7 с по закону I = At2 + B, где А = 0, 1 А/с2, В = 2 А. Определить заряд, прошедший по проводнику.
| q –? | Решение:
Сила тока
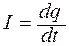 ,
отсюда ,
отсюда
 .
Полный заряд, прошедший по проводнику за время от t1 = 3 c до t2 = 7 с: .
Полный заряд, прошедший по проводнику за время от t1 = 3 c до t2 = 7 с:
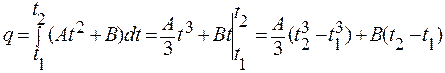 .
Произведем вычисления: .
Произведем вычисления:
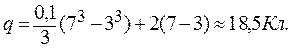 Ответ: q = 18, 5 Кл.
Ответ: q = 18, 5 Кл.
|
| I = At2 + B А = 0, 1 А/с2 В = 2 А t1 = 3 c t2 = 7 с |
Задача 2. Определить плотность тока, если за t = 2 c через проводник сечением S = 1, 6 мм2 прошло N = 2·1019 электронов.
| J –? | Решение:
Плотность тока определяется по формуле
 .
Сила тока .
Сила тока
|
| t = 2 c S = 1, 6 мм2 N = 2·1019 е = 1, 6·10–19 Кл |

отсюда получаем
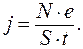
Произведем вычисления:
 .
.
Ответ: j = 104 А/м2.
Задача 3. По медному проводнику сечением S = 0, 8 мм2 течет ток I = 80 мА. Найти среднюю скорость упорядоченного движения электронов < V> проводника, предполагая, что на каждый атом меди приходится один свободный электрон. Молярная масса меди μ = 63, 5 г/моль.
| < V> –? | Решение:
Плотность тока может быть определена по формуле
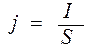 , (1)
с другой стороны, плотность тока связана со скоростью упорядоченного движения электронов формулой , (1)
с другой стороны, плотность тока связана со скоростью упорядоченного движения электронов формулой
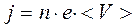 . (2)
Приравнивая эти выражения, получим . (2)
Приравнивая эти выражения, получим
 .
откуда .
откуда
 (3) (3)
|
S = 0, 8 мм2 = 0, 8·10–6 м2
ρ = 8, 9 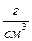 = 8, 9·103 кг/м3
μ = 63, 5·10–3 кг/моль = 8, 9·103 кг/м3
μ = 63, 5·10–3 кг/моль
|
Найдем концентрацию свободных электронов n. Плотность меди может быть определена по формуле
 , (4)
, (4)
где V0 = 1 м3, mа – масса атома меди
 , (5)
, (5)
где NA – число Авогадро.
С учетом (5) формула (4) запишется в виде
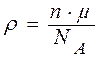 ,
,
откуда
 . (6)
. (6)
Подставим (6) в формулу (3), получим
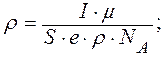
 .
.
Ответ: ρ = 7, 4·10-6 м/с.
 Задача 4. В цепи (рис. 7) амперметр показывает силу тока I = 1, 5 А. Сила тока I1 через сопротивление R1 равна 0, 5 А. Сопротивление R2 = 2 Ом, R3 = 3 Ом. Определить сопротивление R1, а также силу токов I2 и I3, протекающих через сопротивление R2 и R3.
Задача 4. В цепи (рис. 7) амперметр показывает силу тока I = 1, 5 А. Сила тока I1 через сопротивление R1 равна 0, 5 А. Сопротивление R2 = 2 Ом, R3 = 3 Ом. Определить сопротивление R1, а также силу токов I2 и I3, протекающих через сопротивление R2 и R3.
| R1 –? I2 –? I3 –? | Решение:
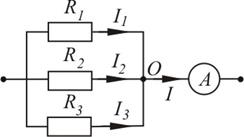 Рис. 8.
Для узла О запишем первое правило Кирхгофа:
I1+ I2+ I3 = I. (1)
Рис. 8.
Для узла О запишем первое правило Кирхгофа:
I1+ I2+ I3 = I. (1)
|
| I = 1, 5 А I1 =0, 5 А R2 = 2 Ом R3 = 3 Ом |
Сопротивления R1, R2 и R3 соединены параллельно, поэтому напряжения на них одинаковы:
I1R1 = I2R2, (2)
I2R = I3R3. (3)
Решим систему уравнений (1) – (3) относительно I2, I3 и R1.
Из (1) выражаем I2:
I2 = I – I1 – I3 (4)
и подставляем в (3)
(I – I1 – I3)R2 = I3R3. (5)
Из уравнения (5) находим I3:
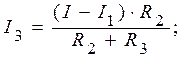
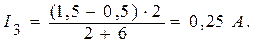
Из уравнения (4) вычисляем I2:
I2 = 1, 5 – 0, 5 – 0, 25 = 0, 75A.
Из уравнения (2) находим R1:


Ответ: I2 = 0, 75 А, I3 = 0, 25 А, R1 = 3 Ом.
Задача 5. Когда к источнику тока подключили резистор сопротивлением R1 = 5 Ом, то сила тока стала I1 = 1 А, а когда подключили резистор сопротивлением R2 = 15 Ом, то I2 = 0, 5 А. Определить ЭДС источника тока, его внутреннее сопротивление и ток короткого замыкания.
| ε –? r –? Iкз –? | Решение:
Дважды запишем закон Ома для полной цепи:
 (1)
Решаем систему относительно r и ε: (1)
Решаем систему относительно r и ε:
|
| R1 = 5 Ом R2 = 15 Ом I1 = 1А I2 = 0, 5 А |
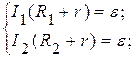 (2)
(2)
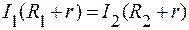 .
.
Отсюда получаем
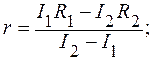
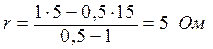 .
.
Зная величину внутреннего сопротивления r, найдем ЭДС источника тока, используя, например, первое уравнение системы (2):
 .
.
Ток короткого замыкания

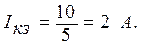
Ответ: ε = 10 В, r = 5 Ом, Iкз = 2 А.

Задача 6. В схеме (рис. 9): R2 = 3 Ом, R1 = R3 = 6 Ом, R4 = 4 Ом, U = 12 В. Найти показание амперметра.
Рис. 9
| I –? | Решение:
Найдем общее сопротивление цепи. Сопротивления R2 и R3 соединены параллельно, их можно заменить сопротивлением R23:
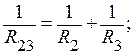
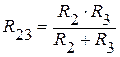 . .
|
| R2 = 3 Ом R1 = R3 = 6 Ом R4 = 4Ом U = 12 В |
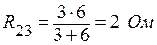 .
.
Последовательное соединение R23 и R4 заменяем сопротивлением R234:
R234 = R23 + R4;
R234 = 2+4 = 6 Ом.
Оставшееся параллельное соединение R1 и R234 можно заменить сопротивлением R1234:
 ;
;
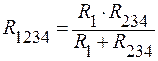 ;
;
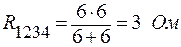 .
.
Теперь схема приняла вид

Рис. 10
Ток через амперметр
 ;
;  .
.
Ответ: I = 4 А.
Задача 7. В схеме, изображенной на рис. 11, ε 1 = 1 В, ε 2 = 1, 3 В, r1 = 3 Ом, r2 = 5 Ом и R = 7 Ом. Найти разность потенциалов между точками А и В, В и С, С и А.
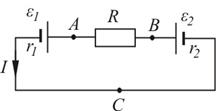
Рис. 11
| φ А – φ В –? φ В – φ С –? φ С – φ А –? | Решение:
Так как источники подключены последовательно одноименными полюсами, то по закону Ома для полной цепи
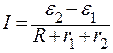 , ,
 .
Разность потенциалов: .
Разность потенциалов:
|
| ε 1 = 1 В ε 2 = 1, 3 В r1 = 3 Ом r2 = 5 Ом R = 7 Ом |
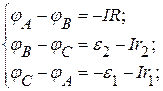

Ответ: φ А − φ В = - 0, 14 В; φ В − φ С = 1, 2 В; φ С − φ А = - 1, 06 В.
Задача 8. Определить сопротивление мотка стальной проволоки диаметром d = 1 мм. Масса проволоки 300 г.
| R –? | Решение:
Сопротивление проволоки
 , (1)
где S - площадь поперечного сечения; , (1)
где S - площадь поперечного сечения;
|
| d = 1 мм = 0, 001 м ρ 1 = 1, 5·10–8 Ом·м ρ 2 = 7, 8·103 кг/м3 m = 300 г = 0, 3 кг |
 . (2)
. (2)
Объем проволоки равен объему цилиндра с основанием S и высотой l
V=S·l. (3)
Масса проволоки
m=V·ρ 2=S·l ρ 2, (4)
отсюда
 . (5)
. (5)
Тогда 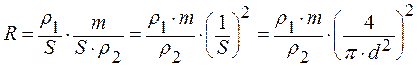 ;
;
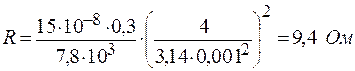 .
.
Ответ: R = 9, 4 Ом.
Задача 9. Вольфрамовая нить электрической лампы при температуре t1 = 2000 oC имеет сопротивление R1 = 204 Ом. Определить ее сопротивление при температуре t2 = 20 oC. Температурный коэффициент сопротивления вольфрама α = 4, 6·10–3 К–1.
| R2 –? | Решение: Учитывая зависимость сопротивления R от температуры t, запишем систему уравнения для двух температур R1 = R0(1 – α t1); (1) R2 = R0(1 – α t2). (2) |
| R1 = 204 Ом t1 = 2000 oC t2 = 20 oC α = 4, 6·10–3 К–1 |
Поделим одно уравнение на другое:

откуда
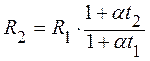 ;
;
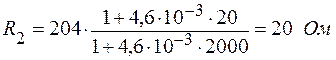 .
.
Ответ: R2 = 20 Ом.
Задача 10. На концах медного провода длиной l = 5 м поддерживается напряжение U = 1 В. Определить плотность тока в проводе.
| j –? | Решение:
Закон Ома в дифференциальной форме для однородного участка цепи
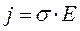 .
Напряженность электрического поля в проводе .
Напряженность электрического поля в проводе
 , ,
|
| l = 5 м U = 1 В ρ =1, 7·10–8 Ом·м |
где U – напряжение, поддерживаемое на концах проводника; l – длина провода.
Проводимость
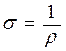 ,
,
тогда  ;
;
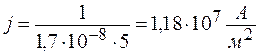 .
.
Ответ: j = 1, 18·107 А/м2.
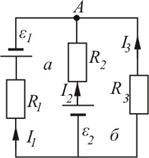
Задача 11. В цепи, изображенной на рис. 12, найти токи через сопротивления R1 = 2 Ом, R2 = 4 Ом, R3 = 2 Ом. ЭДС источников тока равны соответственно ε 1 = 1 В, ε 2 = 3 В, ε 3 = 5 В. Внутренними сопротивлениями источников пренебречь.
Рис. 12.
| I1 –? I2 –? I3 –? | Решение: Для решения задачи используем правила Кирхгофа. 1. Возле каждого сопротивления указываем величину и направление тока (направление выбираем произвольно); 2. Запишем первое правило Кирхгофа для узла А I1 +I2 + I3 = 0; (1) 3. Цепь состоит из двух контуров, обозначенных а и б. Для контура а второе правило Кирхгофа при выбранном направлении обхода по часовой стрелке имеет вид I1R1 – I2R2 = –ε 1 – ε 2. (2) |
| R1 = 2 Ом R2 = 4 Ом R3 = 2 Ом ε 1 = 1 В ε 2 = 3 В ε 3 = 5 В |
Для контура б с тем же направлением обхода
I2R2 – I3R3 = ε 2 + ε 3. (3)
Решаем систему уравнений (1) – (3) методом исключения неизвестных. Из уравнения (1) получаем
I1 = – (I2 + I3). (4)
Подставляя (4) в (2), получаем
(I2 + I3)R1 – I2R2 = –ε 1 – ε 2;
I2R2 + I3R1 + I2R2 = ε 1 + ε 2;
I2(R1 + R2) + I3R1 = ε 1 + ε 2. (5)
Умножив выражение (3) на R1, а выражение (5) на R3, и сложив полученные выражения, получаем
I2R1R2 + I2(R1 + R2)R3 = (ε 2 + ε 3)R1 + (ε 1 ε 2)R3.
Отсюда находим I2:
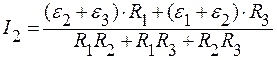 ;
;
 .
.
Из выражения (5) находим I3:
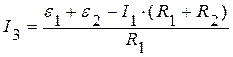 ;
;
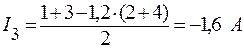 .
.
Из выражения (4) получаем
I1 = –(I2 + I3) = –(1, 2 – 1, 6) = 0, 4 А.
Так как I3 < 0, то реальное направление I3 противоположно указанному на рисунке, а направления токов I1 и I2 совпадают с указанными.
Ответ: I1 = 0, 4 А; I2 = 1, 2 А; I3 = 1, 6 А.