
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Інтегральні 4-вимірні структурні властивості
|
|
Властивості структури. Для оцінки ступеня структуризації зображення або частини, що підлягає декомпозиції, введено ряд параметрів, якими характеризуємо зображення з точки зору його структурних властивостей (індекс позначає рівень), зокрема:
1) Структурні коефіцієнти ступеня трансформації між сусідніми рівнями:
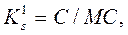
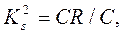
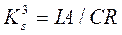 (4.1)
(4.1)
2) Структурні коефіцієнти ступеня трансформації через один сусідній рівень:
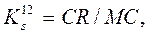
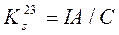 (4.2)
(4.2)
3) Структурні коефіцієнти ступеня трансформації через два сусідні рівні:
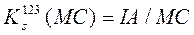 (4.3)
(4.3)
Обернені до коефіцієнтів ступеня трансформації величини назвемо коефіцієнтами ступеня розмитості зображення на різних рівнях ієрархії розбиття зображення, наприклад:
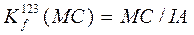 (4.4)
(4.4)
Введемо коефіцієнти ступеня трансформації щодо всієї кількості пікселів PX:
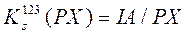 (4.5)
(4.5)
Крім формування структурних особливостей, щоб характеризувати структуру об’єктів (MC, C, CR, ІА), введемо функції питомого об’єму кластера у мікрокластерах або обернену функцію питомої густини кластерів:
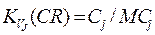 ,
, 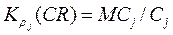 ,
, 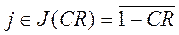 (4.6)
(4.6)
Ці коефіцієнти як питомі характеристики обчислюємо лише для регіонів. Для зв’язних областей вводимо питомі значення як зважені суми відповідних функцій:
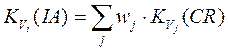 ,
, 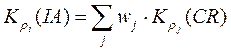 , (4.7)
, (4.7)
де 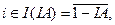
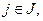 wi = Si (CR) / S (IA), Si (CR) – площа регіона, S (IA) – площа зв’язної області.
wi = Si (CR) / S (IA), Si (CR) – площа регіона, S (IA) – площа зв’язної області.
З рис. 4.2, в видно, що регіони відрізняються між собою за розмірами і визначеними значеннями функції. Маючи функцію 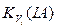 для зв’язної області вводимо питомі функції об’єму та густини для всього образу:
для зв’язної області вводимо питомі функції об’єму та густини для всього образу:
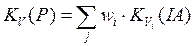 ,
, 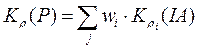 ,
, 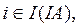 (4.8)
(4.8)
де wi = Si (IA) / S (P), Si (IA) – площа зв’язної області, S (P) – площа образу.
Розглянуті властивості використовуємо для характеристики образу.
Просторові властивості. Розглядаємо статистичні просторові властивості, базовані на структурних властивостях. Для зменшення кількості формул введемо змінну CL (cluster), яка для конкретного ступеня приймає значення CR або IA. Введемо чотири просторових властивості:
1) Середній розмір регіону і зв’язної області:
MS (CL) = (1 / CL)  ∑ Si (CL) (4.9)
∑ Si (CL) (4.9)
2) Середнє квадратичне відхилення розміру регіону і зв’язної області:
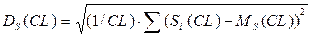 (4.10)
(4.10)
3) Щоб оцінити розмір або середнє квадратичне відхилення елементарного об’єкту образу на різних рівнях декомпозиції пропонуємо наступні статистичні відношення:
 ,
, 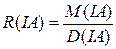 (4.11)
(4.11)
4) Інтегральні статистичні відношення для всього зображення:
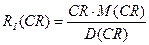 ,
, 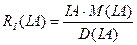 (4.12)
(4.12)
Властивості інтенсивності. Формуємо 8 коефіцієнтів інтенсивності (4× 2) – 4 для кожного ступеня розгляду образу:
1) Середня точкова яскравість регіона і зв’язної області:
BPM (CL) = (1 / CL)  ∑ Bi (CL), (4.13)
∑ Bi (CL), (4.13)
2) Точкове середнє квадратичне відхилення інтенсивності регіону і зв’язної області:
 (4.14)
(4.14)
3) Інтегральна середня зважена яскравість регіону та зв’язної області:
BIM (CL) = ∑ 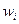 ∙ Bi (CL) (4.15)
∙ Bi (CL) (4.15)
4) Інтегральне середнє квадратичне відхилення зваженої інтенсивності регіону і зв’язної області:
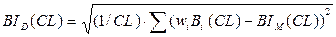 (4.16)
(4.16)
Всі вище розглянуті структурні властивості отримані в результаті роботи розробленого алгоритму триступеневої кластеризації розташовуємо у матрицю інтегральних структурних властивостей:
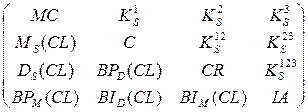 (4.17)
(4.17)
Матриця планується для застосування в алгоритмах класифікації зображень.