
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Рассмотрим пример решения транспортной задачи.
|
|
Пусть имеются 5 пунктов, соединенных между собой дорогами так, что из любого пункта можно проехать в любой другой пункт (рис.2).Известно время перевозки из пункта i в пункт j (табл.1). Требуется найти такой маршрут, начинающийся в данном пункте, проходящий через все пункты и заканчивающийся в пункте выезда, чтобы его продолжительность была наименьшей.

Таблица 1.
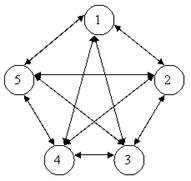
Рисунок 2.
Решение. Для решения этой задачи необходимо составить математическую модель. введем обозначения: i и j – номера пунктов выезда и въезда; tij – время переезда из пункта i в пункт j из таблицы 1 видно, что tij в общем случае может бы не равно времени переезда в обратном направлении tij < > tji (например, когда один пункт на вершине горы, а другой – у ее подножия). Введем булевы переменные:
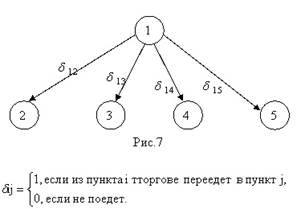
Составим модель (Рис.7). Из пункта 1 можно выехать в любой из пункта 2 или 5, или 3, или 4, или остаться в пункте 1. но при этом можно выехать только в одном единственном направлении. Это условие можно записать так:
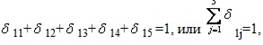 или для производительного i-го пункта
или для производительного i-го пункта 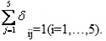
Эти зависимости обеспечивают выполнение условия, что из каждого пункта выезда производится только один раз и только в одном направлении.
Условие въезда в пункт 1 аналогично условию въезда из пункта 1 (Рис.7). Требование минимальной продолжительности маршрута запишется в виде целевой функции:
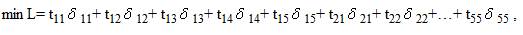
где tij берутся из исходной таблица, а 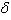 ij - искомые переменные.
ij - искомые переменные.
Тогда всю задачу можно сформулировать:
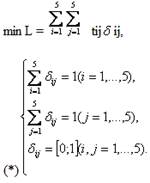
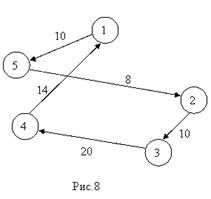
В результате решения системы (*) получим (Рис.8) следующие значения
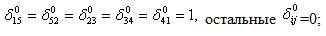

переходя от частной к общей постановке, задачу коммивояжера можно сформулировать как:
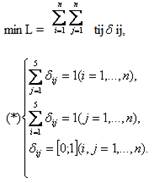
Список литературы:
1. Электронный ресурс: https://pvti.ru/lect1-lecture6.htm
2. Электронный ресурс: https://ru.wikipedia.org/
3. Электронный ресурс: https://www.coolreferat.com
4. Электронный ресурс: https://lmatrix.ru/news/theory/teoriya-grafov-obshhie-svedeniya_35.html