
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Якщо , то рішення
|
|

 , (10.21)
, (10.21)
ЗДР (10.13) при P* (t) 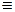 0 і початкових умовах
0 і початкових умовах 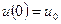 і
і  описує так званий затухаючий аперіодичний рух тіла. Оскільки th bt при
описує так званий затухаючий аперіодичний рух тіла. Оскільки th bt при
t  змінюється в межах від 0 до 1, то з (10.21) витікає, що переміщення u (t) зберігає знак
змінюється в межах від 0 до 1, то з (10.21) витікає, що переміщення u (t) зберігає знак  за умови
за умови 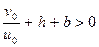 . Цій умові задовольняють точки
. Цій умові задовольняють точки 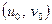 фазової площини, розташовані при
фазової площини, розташовані при  > 0 над прямою v =
> 0 над прямою v =  , при
, при  < 0 — під цією прямою (рис. 10.3). Якщо початкова точка розташована в першому або третьому квадранті фазової площини, то загасання немонотонне (суцільна крива на рис. 10.4), а монотонному загасанню (штрихова крива на рис. 10.4) відповідають області, відмічені на рис. 10.3 горизонтальною штриховкою. Розташування початкової точки в областях з вертикальним штрихуванням (див. рис. 10.3) наводить до загасання із зміною знаку переміщення (штрих-пунктирна лінія на рис. 10.). Якщо
< 0 — під цією прямою (рис. 10.3). Якщо початкова точка розташована в першому або третьому квадранті фазової площини, то загасання немонотонне (суцільна крива на рис. 10.4), а монотонному загасанню (штрихова крива на рис. 10.4) відповідають області, відмічені на рис. 10.3 горизонтальною штриховкою. Розташування початкової точки в областях з вертикальним штрихуванням (див. рис. 10.3) наводить до загасання із зміною знаку переміщення (штрих-пунктирна лінія на рис. 10.). Якщо  , то корні характеристичного рівняння ЗДР (10.14) кратні. Тоді рішення u(t) =
, то корні характеристичного рівняння ЗДР (10.14) кратні. Тоді рішення u(t) = 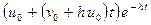 можна отримати з (10.21)
можна отримати з (10.21)

Рис. 10.3 Рис. 10.4
граничним переходом при 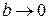 . Цей випадок відповідає лише формальній границі між коливальними і аперіодичними процесами, оскільки реально добитися на практиці точного виконання рівності
. Цей випадок відповідає лише формальній границі між коливальними і аперіодичними процесами, оскільки реально добитися на практиці точного виконання рівності  = h не удається. При
= h не удається. При 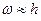 система, виведена з положення рівноваги, найшвидше наближається до нього. Цю властивість використовують при проектуванні амортизаторів і віброзахисних пристроїв, при підборі параметрів заспокоювачів у стрілочних вимірювальних приладах і інших технічних об’єктах.
система, виведена з положення рівноваги, найшвидше наближається до нього. Цю властивість використовують при проектуванні амортизаторів і віброзахисних пристроїв, при підборі параметрів заспокоювачів у стрілочних вимірювальних приладах і інших технічних об’єктах.
Ясно, що всі варіанти рішення ЗДР (10.13), отримані вище при P* (t)  0, залишаться в силі і при P* (t)
0, залишаться в силі і при P* (t)  Р = const, якщо відлік значень
Р = const, якщо відлік значень  і функції u (t) вести від значення и° = Р/с. При зміні зовнішньої сили згідно із законом P* (t)= P
і функції u (t) вести від значення и° = Р/с. При зміні зовнішньої сили згідно із законом P* (t)= P 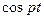 ЗДР (10.13) можна записати у вигляді
ЗДР (10.13) можна записати у вигляді
 .
.
Нескладно перевірити, що цьому ЗДР задовольняє частинне рішення
u (t)=  , де
, де
 ,
,  . (10.22)
. (10.22)
Вигляд амплітудно-частотної А (р) і фазово-частотної  характеристик лінійного осцилятора представлені на рис. 10.5 і не залежить від початкових умов. Абсциса максимуму амплітудно-частотної характеристики при
характеристик лінійного осцилятора представлені на рис. 10.5 і не залежить від початкових умов. Абсциса максимуму амплітудно-частотної характеристики при 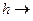 0 прямує до значення
0 прямує до значення  , а ордината максимуму необмежено зростає.
, а ордината максимуму необмежено зростає.
Функція 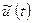 визначає сталий періодичний процес вимушених коливань осцилятора при періодичній зовнішній дії на відміну від вільних коливань, коли відсутня змінна за часом зовнішня дія. Вільні коливання осцилятора залежать лише від характеристик його елементів і початкових умов (в разі гармонійного осцилятора їх зазвичай називають власними коливаннями, оскільки їх кутова частота визначаться рішенням відповідної задачі на власні значення [1]). При h > 0
визначає сталий періодичний процес вимушених коливань осцилятора при періодичній зовнішній дії на відміну від вільних коливань, коли відсутня змінна за часом зовнішня дія. Вільні коливання осцилятора залежать лише від характеристик його елементів і початкових умов (в разі гармонійного осцилятора їх зазвичай називають власними коливаннями, оскільки їх кутова частота визначаться рішенням відповідної задачі на власні значення [1]). При h > 0
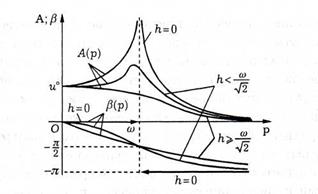
Рис. 10.5
встановленню процесу вимушених коливань передує так званий перехідний процес, тривалість якого залежить від темпу загасання вільних коливань осцилятора. Для лінійного осцилятора це загасання відбувається при t  . Тому тривалість перехідного процесу оцінюють по заданому відносному зменшенню напіврозмахів вільних коливань.
. Тому тривалість перехідного процесу оцінюють по заданому відносному зменшенню напіврозмахів вільних коливань.
Величину D 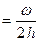 прийнято називати добротністю осцилятора. Чим вище значення D, тим ближче осцилятор до гармонічного. Так, для електричного коливального контуру при частоті
прийнято називати добротністю осцилятора. Чим вище значення D, тим ближче осцилятор до гармонічного. Так, для електричного коливального контуру при частоті 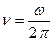 = 104 Гц удається добитися значення D
= 104 Гц удається добитися значення D 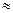 100, для кварцового генератора в електронному годиннику (
100, для кварцового генератора в електронному годиннику ( = 105 Гц) і мікрохвильового об'ємного резонатора
= 105 Гц) і мікрохвильового об'ємного резонатора
( = 1010 Гц) — D = 2 • 104, а для частотно - стабілізованого
= 1010 Гц) — D = 2 • 104, а для частотно - стабілізованого
СО2 - лазера (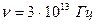 ) — D
) — D  .
.
Кутову частоту  коливань механічного лінійного осцилятора можна виразити через його добротність і кутову частоту
коливань механічного лінійного осцилятора можна виразити через його добротність і кутову частоту  гармонійного осцилятора у вигляді
гармонійного осцилятора у вигляді 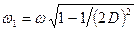 . При високій добротності можна записати
. При високій добротності можна записати  . Ця оцінка справедлива не лише для механічного лінійного осцилятора, але і для електричного коливального контуру і взагалі для будь-якого лінійного осцилятора, в якому відбуваються коливальні процеси довільної фізичної природи.
. Ця оцінка справедлива не лише для механічного лінійного осцилятора, але і для електричного коливального контуру і взагалі для будь-якого лінійного осцилятора, в якому відбуваються коливальні процеси довільної фізичної природи.
Контрольні запитання