
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Связь между непрерывностью и дифференцируемостью функции
|
|
Теорема 20.1. Если функция дифференцируема в некоторой точке, то она непрерывна в ней.
Пусть функция у=ƒ (х) дифференцируема в некоторой точке х. Следовательно, существует предел

Отсюда, по теореме 17.5 о связи функции, ее предела и бесконечно малой функции, имеем ∆ y/∆ x=ƒ '(х)+а, где α → 0 при ∆ х→ 0, то есть ∆ у=ƒ '(х)•∆ х+а•∆ х.
Переходя к пределу, при ∆ х→ 0, получаем

А это и означает, что функция у=ƒ (х) непрерывна в точке х.

Обратная теорема неверна: непрерывная функция может не иметь производной. Примером такой функции является функция
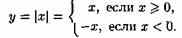
Изображенная на рисунке 131 функция непрерывна в точке х=0, но не дифференцируема в ней. Действительно, в точке х=0 имеем

Отсюда следует, что
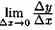
не существует, т. е. функция у=|х| не имеет производной в точке х=0, график функции не имеет касательной в точке O(0; 0).
Замечания: 1. Существуют односторонние пределы функции у=|х| в точке х=0:
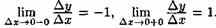
В таких случаях говорят, что функция имеет односторонние производные (или «производные слева и справа»), и обозначают соответственно ƒ '- (х) и ƒ '+(х).
Если ƒ '+(х)≠ ƒ '_(х), то производная в точке не существует. Не существует производной и в точках разрыва функции.
2. Производная у'=ƒ '(х) непрерывной функции у=ƒ (х) сама не обязательно является непрерывной.
Если функция у=ƒ (х) имеет непрерывную производную у'=ƒ '(х) в некотором интервале (a; b), то функция называется гладкой.
28 Применение дифференциала в приближенных вычислениях.
Понятие дифференциала подсказывает, что если какой-Либо процесс по характеру своего изменения близок к линейному, то приращение функции мало отличается от дифференциала. Кроме того, если функция имеет конечную производную в некоторой точке х, то ее приращение и дифференциал также бесконечно малы при  , стремящемся к нулю: , стремящемся к нулю:
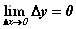 ,
Так как дифференцируемая функция непрерывна, ,
Так как дифференцируемая функция непрерывна,
 Потому что произведение ограниченной функции на бесконечно малую при D X, стремящемся к нулю, есть функция бесконечно малая.
Более того, эти две бесконечно малые функции при
Потому что произведение ограниченной функции на бесконечно малую при D X, стремящемся к нулю, есть функция бесконечно малая.
Более того, эти две бесконечно малые функции при 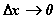 эквивалентны: эквивалентны:

 Эквивалентность
Эквивалентность  и и  дает возможность при малых приращениях аргумента приближенно считать дает возможность при малых приращениях аргумента приближенно считать
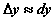 Или
Или

| 29 Дифференциалы высших порядков
Пусть функция  зависит от переменной зависит от переменной  и дифференцируема в точке и дифференцируема в точке  . Может оказаться, что в точке . Может оказаться, что в точке  дифференциал дифференциал 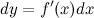 , рассматриваемый как функция от , рассматриваемый как функция от  , есть также дифференцируемая функция. Тогда существует дифференциал от дифференциала , есть также дифференцируемая функция. Тогда существует дифференциал от дифференциала 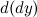 данной функции, который называется дифференциалом второго порядка функции данной функции, который называется дифференциалом второго порядка функции  . Дифференциал второго порядка обозначается следующим образом: . Дифференциал второго порядка обозначается следующим образом:
 Аналогично определяются дифференциалы более высоких порядков.
Дифференциалом
Аналогично определяются дифференциалы более высоких порядков.
Дифференциалом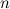 -го порядка -го порядка  функции функции  называется дифференциал от дифференциала называется дифференциал от дифференциала 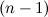 -го порядка этой функции, то есть -го порядка этой функции, то есть
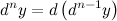 Случай независимой переменной.
Пусть
Случай независимой переменной.
Пусть  - функция независимой переменной - функция независимой переменной  , имеющая дифференциалы любого порядка. Первый дифференциал функции , имеющая дифференциалы любого порядка. Первый дифференциал функции
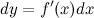 где
где 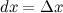 - некоторое приращение независимой переменной - некоторое приращение независимой переменной  , которое мы задаем сами и которое не зависит от , которое мы задаем сами и которое не зависит от  . По определению . По определению
 Переменной является аргумент
Переменной является аргумент  . Значит, для дифференциала величина . Значит, для дифференциала величина 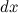 является постоянной и поэтому может быть вынесена за знак дифференциала. То есть дифференциал второго порядка является постоянной и поэтому может быть вынесена за знак дифференциала. То есть дифференциал второго порядка
 Для вычисления дифференциала
Для вычисления дифференциала  применим формулу дифференциала первого порядка к функции применим формулу дифференциала первого порядка к функции  . Тогда получим: . Тогда получим:
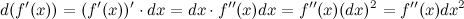 Итак,
Итак,
 Рассматривая последовательно дифференциалы все более высокого порядка, получим формулу дифференциала
Рассматривая последовательно дифференциалы все более высокого порядка, получим формулу дифференциала 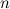 -го порядка: -го порядка:
 Случай зависимой переменной
Пусть задана дифференцируемая функция
Случай зависимой переменной
Пусть задана дифференцируемая функция 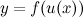 . Тогда . Тогда
 где
где 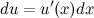 в общем случае не является постоянной величиной. Поэтому дифференциал от функции в общем случае не является постоянной величиной. Поэтому дифференциал от функции  берем как дифференциал от произведения берем как дифференциал от произведения

|
17. Теорема. Если f (x) и g (x) непрерывны в точке x 0, то в этой же точке непрерывны и функции f (x) ± g (x), f (x) × g (x) и f (x)/ g (x) (последнее только в случае, если g (x 0)¹ 0).
Определение. Пусть y = f (x) и x = j(t). Тогда комбинация y = f (j(t)) называется суперпозицией функций f (x) и j(t), или сложной функцией.
Теорема о непрерывности сложной функции.
Пусть x = j(t) непрерывна в точке t 0, а функция f (x) непрерывна в точке x 0= j(t 0). Тогда функция y = f (j(t)) непрерывна в точке t 0.
Короче говоря, суперпозиция непрерывных функций есть также непрерывная функция.