
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Замечательные пределы
|
|
С использованием непрерывности функций можно вывести целый ряд пределов, которые получили общее название замечательных пределов. Ниже приводятся наиболее важные из них.
1.  .
.
- 2.
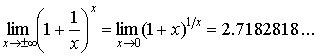
- 3.
 .
. - 4.
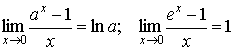 .
. - 5.
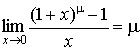 .
. - 6.
 при a > 1 и m> 0.
при a > 1 и m> 0. - 7.
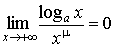 при a > 1 и m> 0.
при a > 1 и m> 0. - 8.
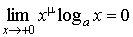 при a > 1 и m> 0.
при a > 1 и m> 0.
18. Определение. Множество не содержащее ни одного элемента называется пустым множеством и обозначается  .
.
В общем случае множества бывают конечные и бесконечные. Определение. Конечное множество это такое множество, для которого существует натуральное число равное числу его элементов.
Например, множество русских букв - конечное множество, так как существует натуральное число 33, равное числу элементов этого множества.
Определение. Множество, не являющееся конечным называется бесконечным множеством. Уже рассмотренное нами множество натуральных чисел  - бесконечное множество, поскольку нет такого натурального числа, которое равнялось бы числу его элементов.Если множество A - конечное множество, то через |A | принято обозначать число его элементов и называть |A | мощностью множества A. Понятие мощности вводится и для бесконечных множеств, однако мы будем рассматривать его немного позднее. Определение. Два конечных множества A и B называются равными, если они состоят из одних и тех же элементов. Если множества A и B равны, то мы будем писать A = B, в противном случае
- бесконечное множество, поскольку нет такого натурального числа, которое равнялось бы числу его элементов.Если множество A - конечное множество, то через |A | принято обозначать число его элементов и называть |A | мощностью множества A. Понятие мощности вводится и для бесконечных множеств, однако мы будем рассматривать его немного позднее. Определение. Два конечных множества A и B называются равными, если они состоят из одних и тех же элементов. Если множества A и B равны, то мы будем писать A = B, в противном случае  Таким образом, мы получили следующее определение: Определение. Два конечных множества A и B не равны между собой, если в множестве A есть элемент не принадлежащий множеству B или наоборот.
Таким образом, мы получили следующее определение: Определение. Два конечных множества A и B не равны между собой, если в множестве A есть элемент не принадлежащий множеству B или наоборот.
Согласно такого определения равенства множеств мы естественно получаем, что все пустые множества равны между собой или что то же самое, что существует только одно пустое множество.
| 36.Общая схема исследования функции и построения графика. Исследование функции у = f(x) целесообразно вести в определенной последовательности. 1. Найти область определения функции. 2. Найти (если это можно) точки пересечения графика с осями координат. 3. Найти интервалы знакопостоянства функции (промежутки, на которых f(x) > 0 или f(x) < 0). 4. Выяснить, является ли функция четной, нечетной или общего вида. 5. Найти асимптоты графика функции. 6. Найти интервалы монотонности функции. 7. Найти экстремумы функции. 8. Найти интервалы выпуклости и точки пере гиб а графика функции. На основании проведенноro исследования построить график функции. Заметим, что приведенная схема исследования не является обязательной. В более простых случаях достаточно выполнить лишь несколько операций, например 1, 2, 7. Если же график функции не совсем понятен и после выполнения всех восьми операций, то можно дополнительно исследовать функцию на периодичность, построить дополнительно несколько точек графика, выявить другие особенности функции. Иногда целесообразно выполнение операций исследования сопровождать постепенным построением графика функции. | 37.наибольшее и наименьшее значение ф-ии на отрезке. наибольшее значение наз-ся самое большое. наименьшее самое меньшее из всех значений ф-ии. Ф-ия может иметь только одно наибольшее и только одно наименьшее или может не иметь их вообще. Правила нахождения наиб и наим значений ф-ии на [а; b]: 1.найти критич. точки ф-ии на интервале (а; b). 2.вычислить значения ф-ии в найденных критич.(.) 3.вычислить значения ф-ии на концах отрезка х=а и х=b. 4.среди всех вычисленных значений ф-ии выбрать наиб и наим. Замечания: 1.если ф-ия y=f(x) на отрезке [a; b] имеет лишь одну критическую (.) и она явл-ся (.) максимума(минимума), то в этой (.) ф-ия принимает наиб(наим) значение. 2.если ф-ия y=f(x) на отрезке [a; b] не имеет крит.(.), то это означает, что на нем ф-ия монотонно возрастает или убывает.следовательно, свое наиб. Значение (М) ф-ия принимает на одном конце отрезка, а наим.(m)-на другом. |
39.осн.приемы интегрирования
1.непосредственное интегрирование.вычисление интегралов с использованием осн. св-в неопределенных интегралов и простейших интергалов наз-ся непосредственным интегрирование.
du=d (u+a); du  ; ;  cosu du=d(sin u), sin u du=-d(cosu);
cosu du=d(sin u), sin u du=-d(cosu);
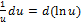 ; ;  2.метод замены.для нахождения интеграла ʃ f(x)dx можно заменить переменную х новой переменной, к-ая связана с х подходящей формулой х=φ (t)
Тогда dx=ϕ ’(t)dt и на основании свойства инвариантности формулы интегрирования неопределенного интеграла получаем формулу интегрирование подстановкой.
2.метод замены.для нахождения интеграла ʃ f(x)dx можно заменить переменную х новой переменной, к-ая связана с х подходящей формулой х=φ (t)
Тогда dx=ϕ ’(t)dt и на основании свойства инвариантности формулы интегрирования неопределенного интеграла получаем формулу интегрирование подстановкой.
 3.Пусть u=u(x) и v=v(x)- функции имеющие непрерывные производные.Тогда d(uv)=u*dv+v*du. Интегрируя это равенство получим:
3.Пусть u=u(x) и v=v(x)- функции имеющие непрерывные производные.Тогда d(uv)=u*dv+v*du. Интегрируя это равенство получим:
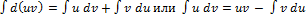 Типы интегралов, которые удобно вычислять методом интегрирования по частям:
1.Интегралы вида:
Типы интегралов, которые удобно вычислять методом интегрирования по частям:
1.Интегралы вида:
 –обозначить все остальные сомножители.
2. –обозначить все остальные сомножители.
2. 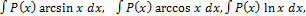
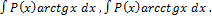 Удобно положить P(x)dx=du, а за u-обозначить остальные сомножители.
3. Удобно положить P(x)dx=du, а за u-обозначить остальные сомножители.
3. 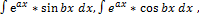 где a и b –числа.За u можно принять функцию u=eax где a и b –числа.За u можно принять функцию u=eax
| 38.первообразная и неопределенный интеграл, его св-ва.таблица интегралов.
Ф-ия F(x) наз-ся первообразной для ф-ии f(x) на промежутке Х, если для любого хϵ Х ф-ия F(x) дифференцируема и выполняется равенство F`(x)=f(x). если производная ф-ии f(x)=0 на промежутке Х, то эта ф-ия постоянна на промежутке Х. пусть F(x)-первообразная для ф-ии f(x) на промежутке Х; тогда любая другая первообразная для f(x) на Х может быть представлена в виде F(x)+C, где С-некоторое число.
Совокупность всех первообразных ф-ий для ф-ии f(x) на промежутке Х, наз-ся неопределенным интегралом от ф-ии f(x) на этом промежутке и обозначается: ʃ f(x)dx=F(x)+C. Операция нахождения первообразной по ее производной или неопределенного интеграла по заданной подынтегральной ф-ии наз-ся интегрированием этой ф-ии. интегрирование явл-ся операцией, обратной дифференцированию.
Св-ва неопределенного интеграла: 1.дифференциал от неопр.интеграла подынтегральному выражению, а производная неопр. интеграла = подынтегральной ф-ии.d(ʃ f(x)dx)=f(x)dx и (ʃ f(x)dx)`=f(x) 2.неопределенный интеграл от дифференциала некоторой ф-ии=сумме этой ф-ии и производной постоянной. ʃ dF(x)=F(x)+C 3. Постоянный множитель можно вынести за знак интеграла.
ʃ a f(x)dx=aʃ f(x)dx а≠ 0.4.неопределенный интеграл от алгебраической суммы конечного числа непрерывной ф-ии=алгебраической сумме интегралов от слагаемых ф-ий. ʃ (f(x)±g(x))dx=ʃ f(x)dx±ʃ g(x)dx. 5. Инвариантность формулы интегрирования.если ʃ f(x)dx=F(x)+C, то ʃ f(u)du=F(u)+C, где u=φ (x)-произвольная функция, имеющая непрерывную производную.
Таблица интегралов:
1. 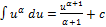 2.
2. 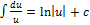 3.
3.  4.
4. 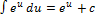 5.
5.  6.
6.  7.
7.  8.
8. 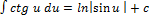 9.
9.  10.
10.  11.
11. 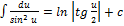 12.
12. 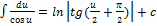 13.
13. 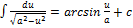 14.
14.  15.
15.  16.
16.  17.
17.  18.
18. 
|
| 9.беск.большаяфункция и их связь с беск. Малой. Если ф-ия f(x) имеет предел, равный А, то ее можно представить как сумму числа А и беск.малой ф-ии α (х), т.е lim f(x)=А, то f(x)=A+α (х). х→ х0 Пусть lim f(x)=А.следовательно Т.е. |f(x)-A-0|< ɛ.Это значит, что ф-ия f(x)-A имеет предел=0, т.е является б.м.ф., к-ую обозначим через α (х): f(x)-A=α (x).Отсюда f(x)=A+α (x). Если ф-ию f(x) можно представить в виде суммы числа А и беск.малой ф- ии α (х), то число А является пределом ф-ии f(x), т.е если f(x)=A+α (x), то lim f(x)=A. Пусть х→ х0 f(x)=A+α (x), где α (x)-б.м.ф. при х→ х0, т.е lim α (x)=0, х→ х0 тогда (ɛ > 0 Ǝ δ > 0 х: 0< |xx0|< δ)→ |α (х)|< ɛ. А так как по условию f(x)=A+α (x), то α (х)=f(x)-A.получаем, (ɛ > 0 Ǝ δ > 0 х: 0< |x-x0|< δ)→ |f(x)-A|< ɛ. А это означает, что lim f(x)=A х→ х0 | |||
| 10.Основные теоремы о пределах. Теорема 1. Предел суммы (разности) двух функций равен сумме (разности) их пределов: Lim f(х) ± ϕ (х)) = lim f(x) ± lim ϕ (х) x→ x0 x→ x0 x→ x0 Пусть lim f(x) = А, lim < ϕ (х) = В. x→ x0 x→ x0 Тогда по теореме 1 о связи функции, ее предела и б. м.ф. можно записать f(x) = А + ɑ (х) и ϕ (х) = В + β (х). Следовательно, f(x) + ϕ (х) = А + В + (ɑ (х) + β (х)). Здесь ɑ (х) + β (х) - б.м.ф. как сумма б. м. ф. Теорема 2 Предел произведения двух функций равен произведеию их пределов: Lim f(х) ± ϕ (х)) = lim f(x) *lim ϕ (х) x→ x0 x→ x0 x→ x0 Доказательство аналогично предыдущему. lim f(x) = А, lim ϕ (x) = В, то x→ x0 x→ x0 f(x) = А + ɑ (х), ϕ (x) = В +β (х), где ɑ (х) и β (х) - б.м. ф. Следовательно, f(x) *ϕ (x) = (А + ɑ (х)). (В + β (х)), т. е. f(x)*ϕ (X) =АB+(A*β (x)+B*ɑ (x)+ɑ (x)β (x)) Выражение в скобках есть б.м.ф. Поэтому lim f(x)•*ϕ (X) = А *В, x→ x0 т. е. lim (f(x)ϕ (x)) = lim f(x) lim ϕ (x). x→ x0 x→ x0 x→ x0 Отметим, что теорема справедлива для произведения любого конечного числа функций. Теорема 3. Предел дроби равен пределу числителя, деленному на предел знаменателя, если предел знаменателя не равен нулю: lim f(x)/ϕ (x)=limf(x)/limϕ (x); (lim ϕ (x)≠ 0). x→ x0 x→ x0 x→ x0 x→ x0 Доказательство аналогично предыдущему. Из равенств lim f(х) = А и lim ϕ (х) = В =1-0 x→ x0 x→ x0 следуют соотношения f(х) = А + ɑ (х) И ϕ (х) = В +β (х). Тогда f(x)/ϕ (x)=A+ɑ (x)/B+β (x)=A/B+(A+ ɑ (x)/ B+β (x)-A/B)=A/B+B*ɑ (x)-A*β (x)/B2+B*β (x). Второе слагаемое есть б.м.ф. как частное от деления б.м.ф. на функцию, имеющую отличный от нуля предел. Поэтому Lim f(x)/g(x)=A/B, т.е. lim f(x)/ϕ (x)=limf(x)/limϕ (x) x→ x0 x→ x0 x→ x0 x→ x0 | |||
54. Скалярное поле. Если каждой точке  пространства ставится в соответствие скалярная величина
пространства ставится в соответствие скалярная величина  , то возникает скалярное поле (например, поле температуры, поле электрического потенциала). Если введены декартовы координаты, то обозначают также
, то возникает скалярное поле (например, поле температуры, поле электрического потенциала). Если введены декартовы координаты, то обозначают также
 или
или 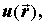
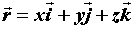 . Поле может быть плоским, если
. Поле может быть плоским, если
 , центральным (сферическим), если
, центральным (сферическим), если 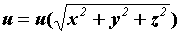 цилиндрическим, если
цилиндрическим, если 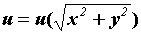 .
.
Поверхности и линии уровня. Свойства скалярных полей можно наглядно изучать с помощью поверхностей уровня. Это поверхности в пространстве, на которых  принимает постоянное значение. Их уравнение:
принимает постоянное значение. Их уравнение: 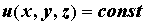 . В плоском скалярном поле линиями уровня называют кривые, на которых поле принимает постоянное значение:
. В плоском скалярном поле линиями уровня называют кривые, на которых поле принимает постоянное значение:  . В отдельных случаях линии уровня могут вырождаться в точки, а поверхности уровня в точки и кривые.
. В отдельных случаях линии уровня могут вырождаться в точки, а поверхности уровня в точки и кривые.
55. Производная по направлению. Пусть  -единичный вектор с координатами
-единичный вектор с координатами  ,
,  - скалярное поле. Производная по направлению характеризует изменение поля в данном направлении и вычисляется по формуле
- скалярное поле. Производная по направлению характеризует изменение поля в данном направлении и вычисляется по формуле 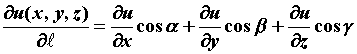 . Производная по направлению представляет собой скалярное произведение вектора
. Производная по направлению представляет собой скалярное произведение вектора  и вектора с координатами
и вектора с координатами  , который называется градиентом функции
, который называется градиентом функции  и обозначается
и обозначается  . Поскольку
. Поскольку  , где
, где
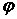 -угол между
-угол между  и
и  , то вектор
, то вектор  указывает направление скорейшего возрастания поля
указывает направление скорейшего возрастания поля  , а его модуль равен производной по этому направлению.
, а его модуль равен производной по этому направлению.
56. Градиент. Производная по направлению представляет собой скалярное произведение вектора  и вектора с координатами
и вектора с координатами  , который называется градиентом функции
, который называется градиентом функции 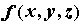 и обозначается
и обозначается 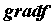 . Поскольку
. Поскольку 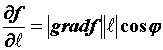 , где
, где
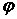 -угол между
-угол между 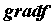 и
и  , то вектор
, то вектор 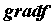 указывает направление скорейшего возрастания функции
указывает направление скорейшего возрастания функции 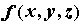 , а его модуль равен производной по этому направлению.
, а его модуль равен производной по этому направлению.
32. ОПРЕДЕЛЕНИЕ. Функция  называется возрастающей (неубывающей) на интервале
называется возрастающей (неубывающей) на интервале  если для любых
если для любых  таких, что
таких, что  значения функции
значения функции  и
и  удовлетворяют неравенству
удовлетворяют неравенству  [1] (
[1] ( ).
).
Функция  называется убывающей (невозрастающей) на интервале
называется убывающей (невозрастающей) на интервале  если для любых
если для любых  таких, что
таких, что  значения функции
значения функции  и
и  удовлетворяют неравенству
удовлетворяют неравенству
 [2] (
[2] ( ).
).
Интервалы возрастания и убывания функции называются интервалами монотонности функции.
Из определения возрастающей функции следует, что если  возрастает на
возрастает на  , то на этом интервале приращение аргумента
, то на этом интервале приращение аргумента  и соответствующее ему приращение функции
и соответствующее ему приращение функции  будут иметь одинаковый знак.
будут иметь одинаковый знак.
Действительно, если 
 , то
, то 
⇒  ,
,
⇒ 
 .
.
Если 
 , то
, то 
⇒  ,
,
⇒ 
 .
.
33. Говорят, что функция f (х) имеет в точке x[0] максимум (минимум), если существует такая окрестность точки x[0], что для всехиз этой окрестности, отличных от x[0], выполняется неравенство
`< `(f(x), f(x[0])) (соответственно `> `(f(x), f(x[0]))).
Иначе говоря, функция f (х) имеет в точке x[0] максимум (минимум), если для достаточно малого приращения Δ х (любого знака) выполняется неравенство `< `(f(`+`(x[0], `*`(Delta, `*`(x)))), f(x[0])) (`> `(f(`+`(x[0], `*`(Delta, `*`(x)))), f(x[0]))).
Максимум и минимум функции называются экстремумом функции.
По определению, максимум и минимум функции могут достигаться лишь внутри области определения, а концы отрезков области определения, не могут служить точками, в которых функция принимает экстремум. Если функция f (х), дифференцируемая в интервале (а; b), имеет в точке x[0], `and`(`< `(a, x[0]), `< `(x[0], b)), экстремум, то ее производная в этой точке равна нулю: (1) Условие (1), будучи необходимым условием экстремума, не является достаточным условием экстремума, что показывает следующий пример.
Пример 1. Функция f(x) = `*`(`^`(x, 3)) не имеет экстремума в точке x[0] = 0 (разность `+`(f(x), `-`(f(0))) меняет знак при изменении знака аргумента х), хотя ее производная y = `+`(`*`(3, `*`(`^`(x, 2)))) обращается в этой точке в нуль.
[1] Иначе говоря, функция  называется возрастающей на интервале
называется возрастающей на интервале  , если большему значению аргумента из этого интервала соответствует большее значение функции.
, если большему значению аргумента из этого интервала соответствует большее значение функции.
[2] Иначе говоря, функция  называется убывающей на интервале
называется убывающей на интервале  , если большему значению аргумента из этого интервала соответствует меньшее значение функции.
, если большему значению аргумента из этого интервала соответствует меньшее значение функции.