
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задача о назначениях
|
|
Задача о назначениях - это одна из задач целочисленного программирования, которая предназначена для оптимального подбора n " предложений" к n " потребностям", например, для назначения вида работы машине, назначения вида работы производственному отделу, назначения человека на должность и т.д. целочисленной называется задача линейного программирования, в которой все компоненты плана х – целые числа.
Метод назначений применяется при решении задач, имеющих следующие характеристики:
1. Имеется n " предметов", которые должны быть распределены по n " пунктам назначения".
2. Каждый " предмет" должен быть назначен единственному " пункту назначения". В понятие " предмет" и " пункт назначения" может вкладываться различное смысловое значение, определяемое конкретной задачей менеджмента. Так в качестве предмета может выступать определенный вид деятельности (работы), должность, человек и т.д.
3. Оптимальный подбор назначений должен быть достигнут за счет максимизации или минимизации определенной меры эффективности назначения: прибыли или стоимости. Для каждого потенциального назначения оценивается мера эффективности. Если мерой эффективности является прибыль, то в процессе решения задачи о назначениях она максимизируется, если мерой эффективности является стоимость, она минимизируется.
В этих задачах задается матрица эффективности (или затрат) действий j-го элемента на i-том объекте. Принимая целочисленные переменные xij равными: xij=1, если j-й элемент действует на i-том объекте, и xij=0 во всех остальных случаях, можно построить для решения задачи следующую модель.
Целевая функция:
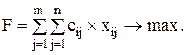 (5.21)
(5.21)
где сij – эффективность действий j-го элемента на i-том объекте.
Ограничения.
1. На каждый объект может быть назначен только один элемент:
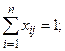
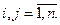 (5.22)
(5.22)
2. Каждый элемент может быть назначен только на один объект:

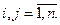 (5.23)
(5.23)
3.
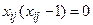
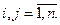 (5.24)
(5.24)
Например, пусть имеется трое рабочих и три производственные операции. Необходимо построить модель расстановки рабочих на участке при условии, что каждый из трех рабочих может выполнять любую из трех операций, и их выработка по операциям характеризуется следующим образом (табл.5.4)
Таблица 5.4- Матрица назначений работников на должности
| Рабочие | ||||
| Опера- | ||||
| ции | ||||
Обозначим хij занятость j-го рабочего на i-той операции. Модель задачи максимизации общей производительности труда будет следующей:
5х11+4х12+6х13+7х21+8х22+5х23+3х31+6х32+5х33→ max
х11+х12+х13=1
х21+х22+х23=1
х31+х32+х33=1
х11+х21+х31=1
х12+х22+х32=1
х13+х23+х33=1
х11+х12+х13=1
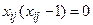
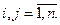 (5.25)
(5.25)
Далее задача может быть решена с использованием диалогового окна «Поиск решения» системы электронных таблиц.
Вопросы для самопроверки:
1. Какова целевая функция и система ограничений классической транспортной задачи?
2. Каким образом осуществляется учет модификаций транспортной задачи?
3. В чем отличия производственно-транспортной задачи?