
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Пример выполнения.
|
|
1. Данные баланса двух отраслей промышленности за некоторый период представлены в таблице баланса:
| Отрасль | Потребление | Конечный продукт | Валовой выпуск | |
2. Оценим продуктивность матрицы прямых затрат.
Составим матрицу прямых затрат: 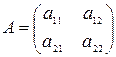 , где
, где 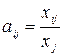 - коэффициенты прямых затрат.
- коэффициенты прямых затрат.
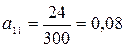 ,
,  ,
, 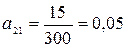 ,
, 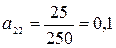 .
.
Значит, 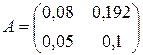 - матрица прямых затрат.
- матрица прямых затрат.
Так как все элементы матрицы А неотрицательны и сумма элементов по любому ее столбцу (строке) не превосходит единицы:
max(0, 272; 0, 15; 0, 13; 0, 292) = 0, 292 < 1,
то по второму критерию продуктивности матрица прямых затрат продуктивна.
Чтобы оценить запас продуктивности, найдем 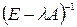 и оценим λ в предположении, что матрица λ А продуктивна.
и оценим λ в предположении, что матрица λ А продуктивна.
Для этого последовательно определяем:
 ,
,
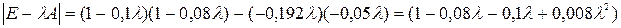 -
-
- 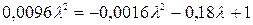 ,
,
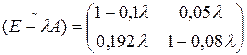 ,
,

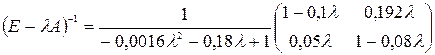 .
.
Для продуктивности последней матрицы необходимо, чтобы все ее элементы были неотрицательны, что возможно при выполнении следующих условий:
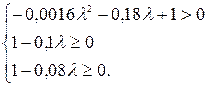
Решаем последовательно каждое неравенство:
| 1) –0, 0016 λ 2- 0, 18λ + 1 > 0, 0, 0016 λ 2+ 0, 18λ – 1< 0. 0, 0016 λ 2+ 0, 18λ – 1= 0 D = 0, 182 + 4·0, 0016 = 0, 0388 λ 1 ≈ -117, 8, λ 2 ≈ 5, 3. | 2) 1 – 0, 1λ ≥ 0 λ ≤ -1/(-0, 1) λ ≤ 10 |
| 3) 1 – 0, 08λ ≥ 0 λ ≤ -1/(-0, 08) λ ≤ 12, 5 |
Окончательно получаем:
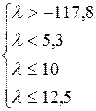 , откуда –117, 8< λ < 5, 3.
, откуда –117, 8< λ < 5, 3.
Таким образом, согласно определению запаса продуктивности, матрица А продуктивна при 1< λ < 5, 3, т.е. запас продуктивности α = 4, 3 – значителен.
3. Найдем новый вектор конечного продукта при увеличении конечного продукта первой отрасли в l = 2, 4 раз, а второй отрасли – на m = 20%.
 .
.
4. Задача межотраслевого баланса формулируется следующим образом: «Найти объем валового выпуска продукции, если конечное потребление по отраслям увеличить соответственно до 547, 2 и 252 усл. ед.»
Новый вектор валового выпуска найдем по формуле:
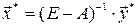 .
.
Последовательно находим:
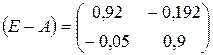 ,
,
Найдем определитель матрицы (Е-А):
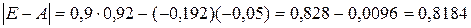 .
.
Составим присоединенную матрицу 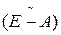 :
:
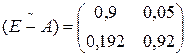 ,
,
транспонировав, получим: 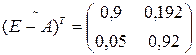
Матрицу 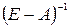 найдем по формуле:
найдем по формуле: 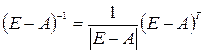 .
.
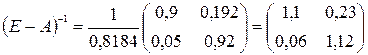 ,
,
Тогда, 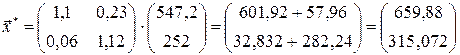 - новый вектор валового выпуска.
- новый вектор валового выпуска.
5. Таким образом, валовый выпуск первой отрасли должен возрасти с 300 усл.ед. до 659, 88 усл.ед., т.е. на 359, 88 усл.ед. (приблизительно на 120%), Валовый выпуск второй отрасли должен возрасти с 250 усл.ед. до 315, 072 усл.ед., т.е. на 65, 072 усл.ед. (приблизительно на 26%).