
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
І. Модель Леонтьєва багатогалузевої економіки
|
|
Лінійні економічні моделі
(балансовий аналіз)
Розглянемо спрощену економіко-математичну модель міжгалузевого балансу. Зв’язок між галузями зазвичай відображають у таблицях міжгалузевого балансу, а математичну модель, яка дає змогу аналізувати їх, розроблено в 1936 р. Американським економістом В.Леонтьєвим.
Припустимо, що весь виробничий комплекс поділено на n „чистих” галузей. Чисті галузі є економічною абстракцією, тобто це умовні галузі, кожна з яких об’єднує все виробництво даного виду продукції. Вважатимемо, що кожна з галузей випускає лише один певний вид продукції (тобто різні галузі випускають різну продукцію). В процесі виробництва кожна з галузей потребує продукції, виробленої в інших галузях.
Мета балансового аналізу – відповісти на запитання, яке постає в макроекономіці й пов’язане з ефективністю ведення багатогалузевого господарства: яким має бути обсяг виробництва кожної з галузей, щоб задовольнити всі потреби в продукції цієї галузі? При цьому кожна галузь виступає, з одного боку, як виробник даної продукції, а з іншого – як споживач і своєї, і виробленої іншими галузями продукції.
Основні припущення моделі, яку надалі називатимемо моделлю Леонтьєва, такі:
1) в економічній системі виробляються, купуються, споживаються і інвестуються n видів продукції, які позначимо індексами 
2) кожна галузь виробляє лише один вид продукції, отже, спільне виробництво різних товарів виключається. Різні галузі виробляють різні товари, й тому галузь, що виробляє продукцію виду i, позначатимемо тим самим індексом;
3) під виробничим процесом у кожній галузі розумітимемо перетворення деяких (можливо всіх) видів продукції, взятих у певних обсягах, на деякий обсяг продукції того чи іншого виду. При цьому припускається, що співвідношення витраченої й випущеної продукції є сталим.
Нехай економіко-виробнича система складається з n галузей, тобто виробляє n видів продукції. Схему міжгалузевого балансу виробництва й розподілу продукції подано в табл. 1, де зазначено основні показники та зв’язки виробництва за певний період часу (зазвичай за рік).
Введемо позначення: Xi – обсяг валової продукції і -ої галузі (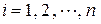 ) за одиницю часу, наприклад за рік; xi j – обсяг продукції і -ої галузі, що потребує j -та галузь у процесі виробництва (
) за одиницю часу, наприклад за рік; xi j – обсяг продукції і -ої галузі, що потребує j -та галузь у процесі виробництва ( ); Yi – обсяг кінцевої продукції і -ої галузі, призначеної для невиробничого споживання.
); Yi – обсяг кінцевої продукції і -ої галузі, призначеної для невиробничого споживання.
Таблиця 1.
| Галузь вироб- ництва | Розподіл випуску продукції в галузях виробництва | Обсяг кінце- вої про- дукції | Обсяг вало- вої про- дукції | ||||||
| ... | j | … | n | Всього | |||||
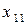
| 
| … | 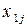
| … | 
| 
| Y1 | X1 | |
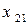
| 
| … | 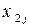
| … | 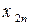
| 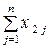
| Y2 | X2 | |
| … | … | … | … | … | … | … | … | … | … |
| i | 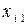
| 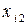
| … | 
| … | 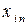
| 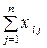
| Yi | Xi |
| … | … | … | … | … | … | … | … | … | … |
| n | 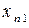
| 
| … | 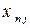
| … | 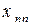
| 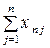
| Yn | Xn |
| Всього | 
| 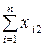
| … | 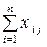
| … | 
| 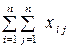
| Y | X |
Використовуючи дані табл. 1, запишемо квадратну матрицю п- ого порядку (за умови рівності поданих у балансі галузей виробництва та споживачів продукції). Кожен елемент матриці xi j, i=1, 2, …, n; j=1, 2, …, n характеризує обсяг поставки продукції з і -ої галузі, що йде на виробниче споживання в j -ій галузі. Взявши суму міжгалузевих поставок продукції і -ої галузі в усіх галузях-споживачах, дістанемо загальний обсяг проміжної продукції і -ої галузі: 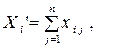 i=1, 2, …, n.
i=1, 2, …, n.
Сума обсягів проміжної продукції всіх галузей виробництва становить загальний обсяг проміжної продукції 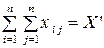 .
.
За економічним змістом обсяг проміжної продукції – частина обсягу валової продукції, яка залишається після вилучення кінцевого продукту й спрямовується для відшкодування поточних матеріальних витрат у межах розглядуваного періоду часу. Оскільки обсяг валової продукції будь-якої і -ої галузі дорівнює сукупному обсягові продукції, що споживається п галузями, та кінцевої продукції, то запишемо систему
 (1)
(1)
або а скороченій формі:
 . (2)
. (2)
Рівняння (1) наз. співвідношеннями балансу.
Розглянемо міжгалузевий баланс у вартісній формі, тобто коли всі величини, що входять у систему (1), виражають вартість.
Особливість системи (1) полягає в тому, що змінні в ній містяться в першому степені, тому залежність між обсягом валової продукції та розподілом продукції кожної галузі лінійна.
Зауважимо, що величини  можуть виражатись в натуральних одиницях (штуках, тоннах, літрах тощо). Тоді йдеться про міжгалузевий баланс у натуральній формі.
можуть виражатись в натуральних одиницях (штуках, тоннах, літрах тощо). Тоді йдеться про міжгалузевий баланс у натуральній формі.
Під час побудови й практичних застосувань економіко-математичної моделі міжгалузевого балансу використовують коефіцієнти прямих матеріальних витрат. Якщо обсяг міжгалузевих поставок і -ої галузі в j -ту поділити на обсяг валової продукції j -ої галузі, дістанемо шуканий норматив:
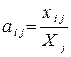 ,
, 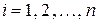 , (3)
, (3)
де  - коефіцієнт прямих витрат продукції і -ої галузі на одиницю обсягу валової продукції j -ої галузі.
- коефіцієнт прямих витрат продукції і -ої галузі на одиницю обсягу валової продукції j -ої галузі.
Ці коефіцієнти утворюють квадратну матрицю коефіцієнтів прямих витрат
 ,
,
яку іноді називають матрицею технологічних коефіцієнтів (технологічною матрицею).
Матриця А містить інформацію про структуру міжгалузевих зв’язків, про технологію виробництва даної економіко-виробничої системи. З рівності (3) випливає, що
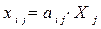 . (4)
. (4)
Підставивши (4) в (3), дістанемо систему
 ,
, 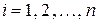 . (5)
. (5)
Запишемо її в матричній формі
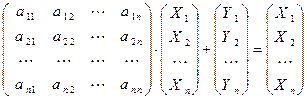 , або
, або
X=AX+Y (6)
Співвідношення (6) називаються рівнянням лінійного міжгалузевого балансу, або моделлю Леонтьєва.
Основна задача міжгалузевого балансу полягає у відшуканні такої матриці обсягів валової продукції Х, яка за відомої матриці прямих витрат А забезпечує задану матрицю обсягів кінцевої продукції Y.
Перепишемо рівняння (6) так:
(E-A)X=Y. (7)
Якщо матриця (Е-А) невироджена, то його можна подати у вигляді
X=(E-A)-1Y. (8)
Матрицю В=(Е – А) - 1 називають матрицею повних витрат.
Економічний зміст елементів матриці В такий: кожен елемент bi j матриці В є обсягом валової продукції і-ої галузі необхідної для забезпечення випуску одиниці кінцевої продукції j-ої галузі(i, j=1, 2, …, n).
За економічним змістом задачі величини Xi мають бути невід’ємними, оскільки Yi ≥ 0 i ai j ≥ 0, де i, j=1, 2, …, n.
З математичного погляду питання про сумісність системи (6) зводиться до питання про існування оберненої матриці (Е – А) – 1, складеної з невід’ємних елементів.
Рівняння міжгалузевого балансу можна використовувати у двох випадках. У першому (простішому) випадку, коли відома матриця обсягів валової продукції X, потрібно обчислити матрицю обсягів кінцевої продукції Y.
Приклад. Нехай матриця обсягів валової продукції галузі й матриця коефіцієнтів прямих витрат мають вигляд:
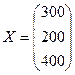 ,
, 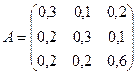 .
.
Використовуючи формулу (7) і правило множення матриць, дістанемо матрицю обсягів кінцевої продукції, що призначена до реалізації:
 .
.
У другому випадку рівняння міжгалузевого балансу використовується для планування.
Матрицю А, всі елементи якої невід’ємні, називають продуктивною, якщо для довільної матриці Y із невід’ємними елементами існує розв’язок рівняння (6) – матриця X, усі елементи якої невід’ємні. В цьому разі модель Леонтьєва називається продуктивною.
Є кілька критеріїв продуктивності матриці А. ми будемо користуватися таким: матриця А з невід’ємними елементами продуктивна, якщо максимум сум елементів її стовпців не перевищує одиниці, причому хоча б для одного із стовпців сума елементів строго менша за одиницю. Тобто матриця А продуктивна, якщо
1. ai j ≥ 0, для довільних i, j=1, 2, …, n;
2.  , i, j=1, 2, …, n;
, i, j=1, 2, …, n;
3. існує номер j такий, що 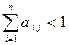 , j=1, 2, …, n.
, j=1, 2, …, n.