
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Приведення експоненційної функції до простої лінійної функції.
|
|
НЕЛІНІЙНІ МОДЕЛІ ТА ЇХ ЛІНЕАРИЗАЦІЯ
Поняття про криві зростання
Криві зростання описують тенденції економічних процесів, наприклад, життєвий цикл товару, процес нагромадження капіталу і т.п.. Найбільше часто в макро- і мікроекономічних дослідженнях використовуються наступні типи кривих:
1) експоненційна: 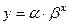 ;
;
2) показникова: 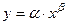 ;
;
3) зворотня: 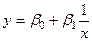
У загальному випадку однофакторну економетричну модель можна представити у вигляді:
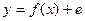 (4.1)
(4.1)
де 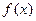 – одна з функцій зростання; е – випадкова величина.
– одна з функцій зростання; е – випадкова величина.
Як і у випадку парної лінійної регресії для моделі (4.1) необхідно знайти невідомі параметри і провести її аналіз.
Приведення експоненційної функції до простої лінійної функції.
Експоненційна функція може бути представлена в наступних еквівалентних формах:
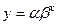 , основна форма
, основна форма 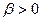 (4.2)
(4.2)
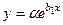 ,
, 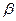 заміняємо на
заміняємо на  , де
, де  (4.3)
(4.3)
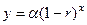 ,
, 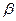 заміняємо на
заміняємо на 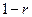 , де
, де 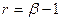 (4.4)
(4.4)
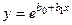 ,
, 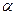 заміняємо на
заміняємо на 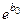 ,
, 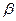 на
на 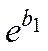 ,
,
де 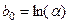 ,
, 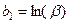 (4.5)
(4.5)
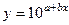 ,
, 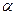 заміняємо на
заміняємо на 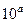 ,
, 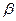 на
на 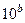 ,
,
де 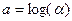 ,
, 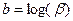 (4.6)
(4.6)
Перераховані форми використовуються на практиці для опису економічних процесів, наприклад форму (4.3) часто використовують у фінансових розрахунках. У цьому випадку 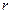 інтерпретується як норма річного відсотка.
інтерпретується як норма річного відсотка.
Для того, щоб визначити невідомі параметри експоненційної кривої необхідно шляхом логарифмічного перетворення звести експонентну криву до лінійної функції, що дасть можливість розрахувати параметри методом найменших квадратів і використовувати подальший аналіз моделі, як і у випадку простої лінійної регресії. Отже, маємо:
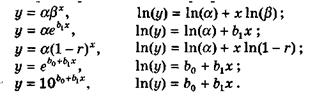
Проводячи необхідну заміну перемінних, переходимо до моделі лінійної регресії, розрахунок параметрів і всі необхідні дослідження якої ми розглядали раніше.