Зворотні перетворення. Приклади їх застосування на практиці

Узагальнена зворотна модель має вигляд:

(4.8)

Вона нелинейна по змінної х, але лінейна по параметрах 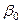і 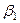і тому є лінійною регресійною моделлю.

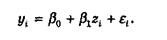Позначимо через , одержимо:

(4.9)

Вибіркова зворотна модель може бути записана у вигляді:

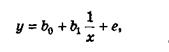
(4.10)

де 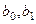– невідомі параметри, які необхідно знайти; – помилка.

Модель (4.10) має свої особливості. При 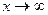, величина , а прагне до граничного значення. Вигляд моделі (4.10) значною мірою залежить від знака параметрів 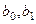(рис. 4.3). Нахил моделі (4.10) визначається за формулою:

.

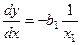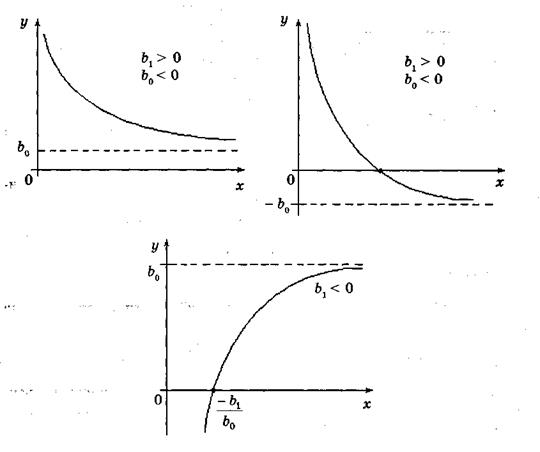
Рис. 4.4. Зворотна функція

Прикладом використання зворотних моделей в економіці є крива Филипса (рис. 4.4). Базуючи на дані норми відсотка зміни заробітної плати і відсотка безробіття для Англії за період з 1861 по 1975 р.м., Филипс побудував криву, наведену на рис. 4.4. Як показано на рис. 4.4 асимптота (границя зміни заробітної плати) зв'язана з параметром 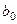. Крапка 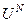є значенням норми безробіття. При 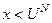норма зміни заробітної плати , при – .

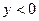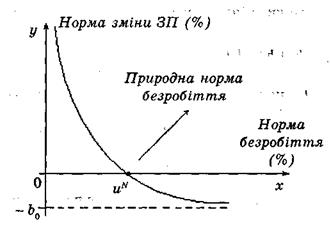
Рис. 4.4. Крива Филипса Рис. 4.5. Крива Энгеля

Крива Филипса дозволяє розрахувати мінімальну заробітну плату, компенсацію по безробіттю й ін..

Інший, не менш важливий приклад використання зворотної моделі – крива витрат Энгеля (рис. 4.5), – зв'язує витрати споживачів на товари з їх загальними витратами чи доходом. Якщо позначити через – витрати споживачів на товари, а через – доход, то за допомогою кривої Энгеля для визначеного товару можна виявити наступні особливості:

а) критичний рівень доходу, нижче якого товар не буде куплений (на рис. 4.5.= );

б) “границю” нагромадження, яку не можна збільшити, як би не ріс доход (на рис. 4.5.= 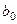).