Степенева (мультиплікативна) функція. Зведення до лінійної регресії. Приклади застосування степеневих функцій у бізнесі і фінансах.

Степенева функція описує дуже широкий спектр економічних процесів. Має наступний вигляд:

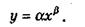(4.7)

Розглянемо випадок, коли параметр а> 0. Для випадку 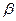– не ціле число, розглянемо лишь випадок, коли 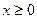. При цьому в залежності від знака параметра 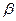степенева функція буде описувати різні економічні процеси: прискорене зростання, уповільнене зростання і спад. Слід зазначити, що якщо 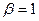, – степенева функція пробразуется в лінійну (див. рис. 4.1 а, б, у, г).

Рис 4.1.Вигляд степеневої функції, якщо 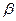– не ціле число,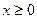

Якщо параметр 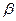– ціле число, то в залежності від того, парне чи непарне його значення, графік функції буде мати різний вигляд. Якщо 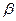-парне, тобто його можна записати у вигляді: 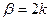, 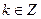(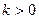), тоді 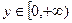[0, +°°), то графік функції симетричний щодо осі ординат (рис. 4.2, а).

Якщо параметр 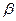– непарне число, тобто його можна представити у вигляді: 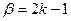, 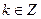(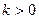), тоді 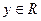, і графік функції симетричний відносно початку координат (0, 0) (рис. 4.2, б).

Рис. 4.2.Графік степеневої функції (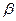 – ціле)

Розрахуємо невідомі параметри степеневої кривої. Покажемо, що за допомогою логарифмічного перетворення ми можемо звести степеневу функцію до лінійної функції, що дає можливість розраховувати параметри методом найменших квадратів. Справді, логарифмуючи праву і ліву частини (4.15), одержимо:

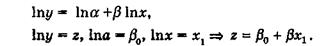
На практиці степеневі функції використовуються для опису різних економічних процесів. Найвідомішої з них є виробнича функція Кобба — Дугласа. Крім того, вони застосовуються для опису криві байдужності, а також попиту на товари різних категорій, так називана крива Торнквиста й ін.