
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Устойчивость
|
|
Итак, будем считать, что аппроксимировать дифференциальные уравнения дискретными аналогами мы научились. Но выясняется, что не каждая разностная схема, полученная в полном соответствии с теорией аппроксимации, позволяет получить разумный результат. Дело в том, что как бы точно ни были заданы начальное приближение, начальные и граничные условия, всегда найдется какая-нибудь погрешность. Как минимум будут ошибки округления. При некоторых условиях эти ошибки начинают быстро расти. В конце концов, это может привести к тому, что результат опять не будет ничего общего иметь с моделируемым процессом.
Условие, что погрешности не накапливаются, называется условием устойчивости. Существует много методов проверки различных численных схем на устойчивость. Рассмотрим два из них.
Первый способ не очень точен, применение его бывает довольно громоздким, но он интуитивно понятен и надежен. Называется методом дискретного возмущения [9]. В методе предполагается, что во всех узлах решение точное, кроме одного, в котором возмущение равно d. Далее следят за развитием этого возмущения и пытаются выяснить, при каких условиях оно нарастает.
Начнем с простого уравнения первого порядка. Рассмотрим решение волнового уравнения схемой «уголок». Итак, имеем разностную схему
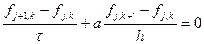
откуда выражаем значение на новом слое

Безразмерный комплекс 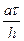 называется числом Куранта и обычно обозначается C. Теперь выражение для значения на следующем слое можно записать более кратко
называется числом Куранта и обычно обозначается C. Теперь выражение для значения на следующем слое можно записать более кратко
fj+1, k=(1+C)fj, k-Cfj, k+1
В силу линейности уравнения возмущения будут описываться таким же соотношением. Для доказательства представим значение в каждой точке в виде суммы точного решения реально решаемого уравнения (будем обозначать его звездочкой) и погрешности.


Вычитая из данного соотношения уравнение для точного решения получаем
 δ j+1, k=(1+C)δ j, k-Cδ j, k+1
δ j+1, k=(1+C)δ j, k-Cδ j, k+1
Считаем, что на j-м слое все возмущения, кроме k-го, равны нулю. Возмущение в k-й точке равно d. Тогда на j+1-м слое будут два ненулевых возмущения:
dj+1, k-1=-Cd
dj+1, k=(1+C)d
Чтобы схема была устойчивой, требуется, чтобы максимальное по модулю возмущение на новом слое было меньше или равно максимальному по модулю возмущению на предыдущем слое. Из соотношения для k-1-го узла получаем: |C|£ 1. Из соотношения для k-го узла имеем: -2£ C£ 0. Следовательно: -1£ C£ 0. Теперь рассмотрим k+2-й слой. Там будут три ненулевых возмущения:
dj+2, k-2=-C2d
dj+2, k-1=-2C(1+С)d
dj+1, k=(1+C)2d
Их надо сравнить с максимальным по модулю возмущением из j+1-м. Желающие могут убедиться, что новых ограничений мы не получим. Не получим их и если рассмотреть последующие слои. Окончательно имеем: ‑ 1£ C£ 0. Так как шаги по времени и по пространству положительны, то получаем, что использовать такую схему можно только при a£ 0. Причем шаг по времени должен удовлетворять соотношению
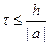
Все это было проделано для схемы, где производная по пространству аппроксимировалась разностью вперед. Все тоже самое можно проделать для схемы с разностью назад. Желающие могут проделать такие же выкладки. Я здесь привожу конечный результат: 0£ C£ 1. То есть «левый уголок» для этого уравнения можно применять только при положительных a.
Применение метода дискретного возмущения для неявных схем затруднительно.
Условие |C|£ 1 называется условием Куранта-Фридрихса-Леви. Вообще говоря, это условие является необходимым (но не достаточным!) для всех явных схем для дифференциальных уравнений гиперболического типа.
У полученных результатов (в том числе и у условия Куранта-Фридрихса-Леви) есть несколько трактовок и интерпретаций. Рассмотрим сначала интерпретацию с помощью характеристик. Здесь полезно графическое изображение. Сначала мы рассматривали «правый уголок». Проведем характеристику через точку на новом слое. Рассмотрим неустойчивые случаи: a> 0 и |C|> 1. Характеристика показана на рисунке красным цветом

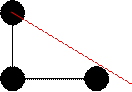
А теперь посмотрим, как выглядит картинка для устойчивого случая

Из рисунков очевидно следует простая интерпретация: характеристика, приходящая в точку, где мы хотим найти значение, должна пересекать отрезок, соединяющий какие-либо две другие точки в используемом шаблоне. Как отмечалось выше, характеристика идущая в точку, где нужно найти значение, должна приходить из области, где значение известно. В данном случае, такой областью является отрезок, соединяющий две точки, используемые в шаблоне (на отрезке всегда можно найти значение с помощью интерполяции).
Еще одна интерпретация условия Куранта-Фридрихса-Леви гласит: численное возмущение должно распространяться по сетке не медленнее, чем распространяется в пространстве возмущение в моделируемом процессе. Так, в рассмотренном примере возмущение, заданное в одной точке на слое, на следующем слое было уже и в соседней точке. То есть за время t оно распространилось в пространстве на расстояние h. Таким образом, скорость распространения численного возмущения составила 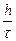 . Для устойчивости эта скорость должна быть больше или равна физической скорости a. Нетрудно заметить, что это и утверждается условием Куранта-Фридрихса-Леви.
. Для устойчивости эта скорость должна быть больше или равна физической скорости a. Нетрудно заметить, что это и утверждается условием Куранта-Фридрихса-Леви.
При использовании схемы «левый уголок» картинки симметричны рассмотренным. Отсюда следует простое правило: при использовании схемы типа «уголок» нужно использовать разность навстречу потоку (против потока).
Самым популярным методом исследования разностных схем на устойчивость является спектральный признак устойчивости (он же метод фон Неймана). Он точен для линейных уравнений с постоянными коэффициентами. Итак, будем искать ошибку в виде

это соответствует представлению функции ошибки в виде интеграла Фурье. При этом G отвечает за амплитуду колебаний, а q - за период колебаний. Требование устойчивости сводится к условию
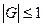
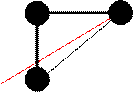
при любых значениях q. Рассмотрим применение этого метода к неявным схемам типа «уголок» для волнового уравнения первой степени. Возьмем разностную схему вида
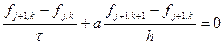
подставляем выражение для ошибки
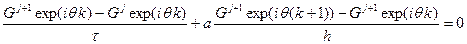
сокращая на Gj exp(iθ k) получаем
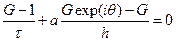
преобразуем выражение

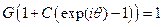
из условия устойчивости получаем
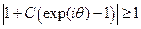
Построим на комплексной плоскости возможные значения левой части полученного выражения. Геометрическое точек  представляет собой окружность единичного радиуса с центром в точке -1. Выражение, стоящее под модулем, описывает окружность радиусом C с центром в точке 1-C. Таким образом, получаем следующее графическое представление
представляет собой окружность единичного радиуса с центром в точке -1. Выражение, стоящее под модулем, описывает окружность радиусом C с центром в точке 1-C. Таким образом, получаем следующее графическое представление
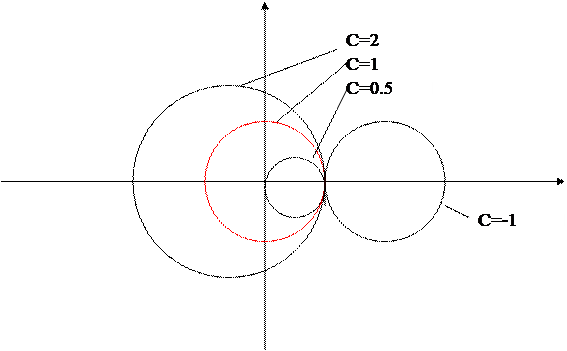
Отсюда наглядно видно, что при С=1 получаем единичную окружность, т.е. неравенство превращается в равенство. Это означает, что величина ошибки будет оставаться на прежнем уровне (не будет расти, но и не будет уменьшаться). Неравенство выполняется при С£ 0 и при С³ 1. При 0< C< 1 схема неустойчива.
Дадим другую графическую интерпретацию полученного результата. Проведем характеристику через одну из точек на новом слое. Получаем


C< 0 0< C< 1 C> 1
Совершенно аналогично можно рассмотреть другую неявную схему
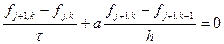
Естественно, получим устойчивость при С£ -1 и при С³ 0. При -1< C< 0 схема неустойчива. Видно, что обеспечить устойчивость неявных схем гораздо проще. Так, если использовать схемы с разностью против потока, то такие схемы будут устойчивы при любом модуле числа Куранта. Такие свойства неявных схем обеспечили им широкое применение.
Рассмотрим теперь устойчивость разностных схем для параболических уравнений. В них возмущения распространяются с бесконечно большой скоростью. В принятой в данной писанине графической интерпретации характеристики параболических уравнений вырождаются в горизонтальные линии. Может показаться, что из этого следует неустойчивость всех явных разностных схем для параболических уравнений. Но, как отмечалось выше, разностные схемы описывают не исходные уравнения, а некоторые другие. Эти другие уравнения могут иметь совершенно иные свойства. Обычно этот факт приносит сплошные неприятности. Но нет худа без добра. Реально решаемые уравнения могут оказаться не параболическими а гиперболическими, а для таких явные схемы могут быть устойчивыми.
Ранее рассматривалась явная разностная схема для цветового уравнения
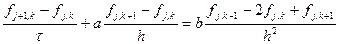
Применим метод фон Неймана для анализа ее устойчивости.

Проведем ряд сокращений

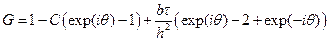
комплекс  не имеет общепринятого названия, для краткости будем обозначать его через D. Воспользуемся также формулой Эйлера
не имеет общепринятого названия, для краткости будем обозначать его через D. Воспользуемся также формулой Эйлера
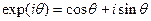
Тогда имеем

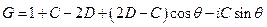
Геометрическое место таких точек на комплексной плоскости будет представлять собой эллипс с центром в точке 1+C-2D. Полуось в направлении оси X равна |2D-C|, а полуось в направлении оси Y равна С. В соответствии с условием устойчивости этот эллипс не должен выходить за пределы единичной окружности. Из рассмотрения пересечения эллипса с осями координат следует: |C|£ 1 и -1£ C-2D£ 0. Еще одно ограничение возникает из рассмотрения радиуса кривизны эллипса в точке касания с единичной окружностью: С2£ |2D-C|. Все четыре возможных варианта эллипсов, соответствующих неустойчивым схемам представлены на рисунке (единичная окружность показана красным цветом).

Проанализировав эти ограничения, можно оставить только два из них (остальные выполнятся автоматически): 2D£ C+1 и C2+C£ 2D. К ним можно добавить, что для уравнений, описывающих реальные процессы в плазме величина D всегда положительна, т.к. положительны все величины, входящие в ее определение.
Теперь рассмотрим эти ограничения с точки зрения шагов по пространству и времени. Перепишем второе ограничение в виде

разделив полученное равенство на шаг по времени и умножив на квадрат шага по пространству получаем:

После несложного преобразования получаем
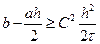
Ранее было показано, что то, что стоит в левой части полученного неравенства, является коэффициентом вязкости (теплопроводности, диффузии) в реально решаемом уравнении. В правой части неравенства стоит заведомо неотрицательная величина. Таким образом, это условие устойчивости можно сформулировать так: в реально решаемом уравнении (еще точнее: в дифференциальном приближении) коэффициент вязкости (теплопроводности, диффузии) должен быть неотрицательным[10]. Это же неравенство можно рассматривать как ограничение на шаг по пространству. Таким образом, при численном решении параболических уравнений с использованием явных схем существуют не только ограничения на шаг по времени, но и ограничения на шаги по пространству.
Такое ограничение на шаг можно снять, если для аппроксимации первой производной по пространству использовать центральную разность. Ранее было показано, что коэффициент вязкости (теплопроводности, диффузии) при этом не меняется в зависимости от шага. Проверяем. Запишем разностную схему

Применим метод фон Неймана для анализа ее устойчивости.
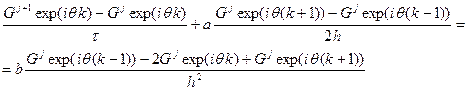
Проведем ряд сокращений
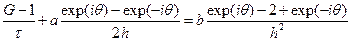
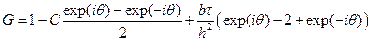

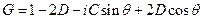
Геометрическое место таких точек на комплексной плоскости будет представлять собой эллипс с центром в точке 1-2D. Полуось в направлении оси X равна 2D, а полуось в направлении оси Y равна С. В соответствии с условием устойчивости этот эллипс не должен выходить за пределы единичной окружности. Из рассмотрения пересечения эллипса с осями координат следует: |C|£ 1 и 0£ D£ 0.5. Еще одно ограничение возникает из рассмотрения радиуса кривизны эллипса в точке касания с единичной окружностью: С2£ 2D. Подставив в последнее неравенство вместо безразмерных чисел их определения, получаем

откуда
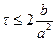
Теперь рассмотрим ограничение на величину D
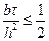
откуда

Таким образом, ограничение на шаг по пространству снято, зато появились два новых ограничения на шаг времени. Следует отметить, что одно из этих ограничений не зависит от шага по пространству и определяется только физическими величинами.
Давненько в этом тексте не упоминались эллиптические уравнения. Ранее писалось, что для их решения вводят новую переменную и сводят задачу к решению параболического уравнения. Рассмотрим, как это происходит, на примере уравнения Лапласа.
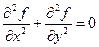
Превращаем его в параболическое уравнение
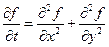
Напишем разностную схему
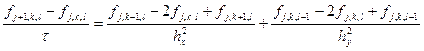
Применим метод фон Неймана (теперь в нем будут фигурировать две экспоненты и две переменные, отвечающие за периоды колебаний)

сокращая получаем

Применяя формулу Эйлера получаем

Схема будет устойчивой, если модуль G будет меньше единицы при любых значениях q и j. Отсюда легко получаем
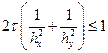
или

Если шаги по обоим пространственным направлениям равны, то формула упрощается
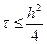
Теперь рассмотрим, что станет с рассмотренной разностной схемой, если в нее подставить максимальное допустимое значение шага по времени.

Перенесем все члены из левой части в правую. Получим

Как видно, такое уравнение соответствует разностному аналогу исходного уравнения (до введения дополнительной переменной) у которого значение центрального элемента взято на новом слое. Новая переменная уже не присутствует в разностной схеме, поэтому обычно говорят не о слоях по времени, а об итерациях.
Выразим явным образом значение функции на новой итерации
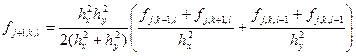
В случае если шаги по разным направлениям равны, то формула становится еще проще
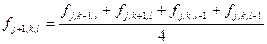
т.е. в этом случае новое значение функции в узле равно среднему арифметическому значений в соседних узлах.
До сих пор мы рассматривали отдельные уравнения. Теперь надо упомянуть системы уравнений. Рассмотрим простейшую систему дифференциальных уравнений.

Используем явную схему типа «уголок»

Воспользуемся спектральным методом для анализа устойчивости. Запишем в матричной форме.

Умножим на шаг по времени и перенесем первый вектор-столбец в правую часть

Вектор-столбцы представляют собой погрешности на текущем и следующем шагах по времени. Линейная алгебра учит, что существуют такие числа l, что погрешность на новом слое будет ровно в l раз больше погрешности на текущем. Критерием устойчивости при этом гласит: максимальный модуль l не должен превосходить 1. Согласно той же самой алгебре для нахождения таких чисел приравниваем нулю определитель матрицы
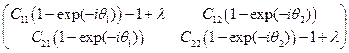
получаем квадратное уравнение
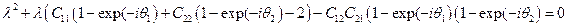
Это уравнение, конечно, можно решить аналитически, после чего тщательно исследовать условия устойчивости. Но в случае, когда имеется несколько нелинейных уравнений (типичная ситуация при расчетах плазмы), задача может стать нерешаемой в принципе.
Следует вспомнить, что метод фон Неймана точен для линейных уравнений с постоянными коэффициентами. К тому же, все что до сих пор рассматривалось, никак не учитывало граничные условия, а они (в некоторых случаях) тоже могут влиять на устойчивость.
Как обычно, если нам неизвестно точное решение (в данном случае точные ограничения по устойчивости), но известны оценки (анализ устойчивости разностных схем по описанным выше методикам для отдельных уравнений), то все, что неизвестно, учитывают некоторым эмпирическим коэффициентом. Делается это чрезвычайно просто. Если за tс обозначить шаг по времени, полученный из анализа устойчивости уравнений поодиночке (возможно даже упрощенных уравнений), а за a - коэффицент, то шаг по времени выражается так
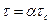
Такой подход называется релаксацией. Если a< 1, то говорят о нижней релаксации, если a> 1, то – верхней. Рассмотрим применение такого подхода к решению уравнения Лапласа (шаги по пространственным направлениям будем считать одинаковыми).
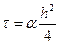
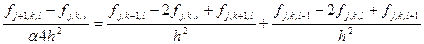
умножаем на знаменатель дроби в левой части, получаем

обозначив за f* решение, получаемое без релаксации, получаем часто используемую формулу
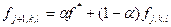
То есть решение линейно выражается через значение на текущем слое и значение, полученное по каким-то из ранее рассмотренных формул. В таком виде релаксация, как правило, и применяется.
Нижняя релаксация повышает устойчивость, но увеличивает число шагов по времени (итераций). Верхняя релаксация наоборот снижает устойчивость, но уменьшает число шагов. На практике оптимальное значение коэффициента подбирают экспериментально. Иногда использование релаксации позволяет существенно (до десятков раз) сократить время счета или сделать устойчивым разваливающийся расчет.