
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Аналитические решения
|
|
Прежде, чем заняться рассмотрением конкретных численных методов, посмотрим на некоторые из аналитических решений уравнений, описывающих процессы в плазме. Все они получены при некоторых предположениях и упрощениях. Об этом нужно вспоминать всякий раз, когда пытаешься воспользоваться полученной формулой. Необходимо всегда проверять, насколько применимы к рассматриваемому случаю эти самые допущения.
Задача 1. Рассмотрим одномерную стационарную задачу прохождения электронного тока через область с магнитным полем. Необходимо найти градиент электрического поля, обеспечивающий прохождение электронов с заданной средней скоростью и постоянной концентрацией. Итак считаем, что нам дано:
n0 – концентрация нейтральных частиц,
B – индукция магнитного поля,
ux - средняя скорость электронов,
< sovo> - скорость упругих столкновений электронов с нейтральными частицами.
Задача решается при следующих предположениях:
- средняя скорость потока электронов много меньше тепловой скорости электронов,
- характерный размер задачи много больше радиуса Лармора электронов,
- параметр Холла много больше единицы,
- энергию электронов считаем постоянной,
- течение ламинарное,
- диффузия электронов через магнитное поле определяется упругими столкновениями электронов с нейтральными частицами.
При использовании магнитогидродинамической модели плазмы получается следующая система уравнений:

С учетом того, что все производные по x (кроме электрического потенциала) равны нулю, и на постоянную концентрацию можно поделить, получаем:

Откуда находим искомый градиент потенциала электрического поля:

Следует отметить, что в практических задачах очень часто невыполняется одно или несколько из указанных выше предположений. В таких случаях применять полученную формулу нельзя.
Задача 2. Найти скорость ионов на границе плазма-пристеночный слой. Первым делом надо сказать, что никакой четкой границы там, конечно же, нет, и никогда не было. Под границей будем понимать некоторую условную поверхность, по одну сторону которой плазму можно считать квазинейтральной, а по другую – нет.
Основные предположения:
- радиус Дебая много меньше длины пробега электронов до ионизации,
- магнитное поле отсутствует или радиус Лармора много больше радиуса Дебая,
- электроны имеют Максвелловское распределение по скоростям.
Рассмотрим «окрестность границы плазма-слой». Индексом b будем обозначать значение на границе плазма-слой. В плазме концентрации ионов и электронов совпадают, поэтому никакого индекса им давать не буду. Итак, для ионов имеем
nui=nbuib.
Выберем начало отсчета потенциала так, чтобы энергию ионов можно было записать формулой
-eφ =Mui2/2.
Из нее получаем, что при незначительном изменении потенциала концентрация ионов описывается соотношением
ni=nb  .
.
Считая изменения потенциала незначительными можно упростить формулы для концентраций
ni=nb(1+Δ φ /2φ b),
ne=nb(1+e Δ φ /(kTe)).
Уравнение Пуассона для электрического потенциала при этом можно записать в виде
d2φ /dx2=(enb/ε 0)[(e/kTe)-(1/2φ b)]Δ φ.
Так как известно, что вторая производная потенциала отрицательна, получаем
-φ >  .
.
В силу нашего определения потенциала на границе имеем
uib= 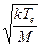 .
.
Согласно литературным источникам [6] изначально эта формула была выведена Тонксом и Ленгмюром, а затем приведенный здесь упрощенный вывод был сделан Бомом. Теперь эта формула носит его имя.
Задача 3. Определить пристеночный перепад потенциала в зависимости от средней скорости электронов. В этой задаче граница плазма-слой понимается в том же смысле, что и в предыдущей. Основные предположения:
- толщина приэлектродного слоя много меньше радиуса Лармора для электронов,
- можно пренебречь процессом ионизации,
- кинетическая энергия потока электронов в плазме много меньше его полной энергии (на границе плазма-слой можно пренебречь кинетической энергией электронов),
- в связи с малой толщиной рассматриваемого слоя теплопроводность плазмы приводит к выравниванию температуры поперек слоя (изменением температуры можно пренебречь).
На основании этих предположений можно записать следующие соотношения:
- уравнение сохранения массы
neue=const
- уравнение сохранения импульса

уравнение сохранения энергии
Te=const
Из первых двух уравнений получаем

Проинтегрировав получаем

Приняв потенциал границы плазма-слой за нулевой, с учетом сделанных предположений можно получить выражение для константы в уравнении
С= 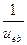
где u eb - скорость электронов на границе плазма-слой.
Подстановка дает
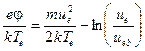
Дифференцирование по ue дает

Из этого следует, что зависимость потенциала от скорости электронов имеет экстремум при
ue= 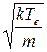
Это означает существование минимального потенциала, при котором еще возможно прохождение такого потока электронов. Приняв этот потенциал за потенциал стенки, можно получить выражение для величины пристеночного скачка потенциала
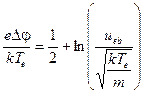
Следует заметить, что при различных изменениях исходных предположений можно получить аналогичные формулы, отличающиеся от данной константой в правой части.
Задача 4. Определить массовый расход при истечении разреженного газа из полости в вакуум через маленькое отверстие в тонкой стенке. Здесь будет приведен до предела упрощенный вывод формулы. Главное упрощение заключается в том, что вместо учета распределения частиц по скоростям, мы будем считать все частицы имеющими одну «тепловую» скорость. Распределение частиц по направлениям в районе отверстия будем считать равномерным.
Введем сферическую систему координат. Начало координат расположим в центре отверстия. Ось Х направим перпендикулярно стенке в сторону вакуума. Угол между каким-либо выбранным направлением и осью обозначим a. Интересующий нас поток, создаваемый частицами с заданным направлением будет пропорционален косинусу a. Отсюда получаем формулу для массового потока
Amnv  =Amnv
=Amnv  =Amnv/4
=Amnv/4
где А – площадь отверстия.