
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Метод конечных разностей
|
|
Существует множество численных методов решения дифференциальных уравнений. Некоторые из них ищут решение в виде аналитических функций. Однако, для случаев со сложной геометрией или разрывами в граничных условиях такие методы становятся довольно громоздкими. Поэтому большинство численных методов решения дифференциальных уравнений рассматривают дискретно заданные («сеточные») функции, т.е. функции, заданные на некотором множестве точек, называемом сеткой.
Поговорим о сетках. В одномерном случае от сетки остается лишь конечное множество точек, заданное на отрезке, на котором ищется решение. Точки могут располагаться равномерно или неравномерно. В многомерном случае наблюдается огромное многообразие типов сеток. Приведем лишь несколько примеров. Ниже на рисунках представлены равномерные прямоугольная и треугольная сетки.


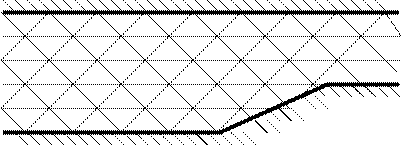
Сетки бывают неравномерными (часто линии сетки сгущают в той области, где хотят поднять точность расчета).

Сетки бывают адаптивными (например, сетка, являющаяся прямоугольной в некоторой системе координат, связанной с поверхностью).

Правильный подбор типа и параметров сетки может существенно (в отдельных случаях на порядки) сократить ресурсы, требуемые для получения результата.
Точки пересечения линий сетки называются узлами. Элементарные области, ограниченные линиями сетки (плоскостями или иными поверхностями в трехмерном случае) называются ячейками. Значения искомой функции могут задаваться либо в узлах сетки, либо в каких-либо точках (например, в центрах) ячеек.
Численные методы решения дифференциальных уравнений, работающие с сеточными функциями, сводят исходную задачу к решению системы алгебраических уравнений. Одним из самых распространенных методов является метод конечных разностей[7]. Ему будет посвящена значительная часть данного курса. Не потому, что он лучший. Просто когда-то он был самым распространенным и по нему написано огромное количество книг, в которых изложены все трудности, которые встречаются и в других методах. Например, можно почитать книжки [9, 10]. Как правило, для метода конечных разностей используют прямоугольные сетки. Значения функции рассчитываются в узлах сетки.