
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Классификация моделей плазмы
|
|
Курс численных методов моделирования плазмы
Дурака учить – что мертвого лечить.
(Народная мудрость)
Введение
О том, сколько существует различных типов плазмы, рассказывается в других курсах. Я, признаюсь, со счету сбился. Желающие могут посмотреть в умных книжках, например [1]. Здесь упомяну лишь несколько признаков, по которым чаше всего классифицируют задачи по моделированию процессов в плазме:
- количество типов рассматриваемых частиц;
- отношение длины пробега частиц к характерному размеру задачи (число Кнудсена);
- влияние магнитного поля на рассматриваемые процессы, соотношение индукций магнитного поля создаваемых внешней магнитной системой и токами в плазме;
- отношение радиусов Дебая и Лармора к характерному размеру задачи;
- влияние лучистого энергообмена на рассматриваемые процессы;
- зависимость процессов от времени.
Для каждой комбинации перечисленных признаков нужно рассматривать свои математические модели.
Сколько существует численных методов для описания процессов в плазме – вообще учету не поддается. Мне, во всяком случае, даже никогда не приходилось видеть сколь бы то ни было «полный» список таких методов[1]. Ситуация осложняется отсутствием общепризнанных названий известных методов и тем, что одни и те же методы в разных источниках называются по-разному. Часто под одним и тем же названием в разных книгах скрываются совершенно разные методы.
Даже то, что знаю я, изложить на должном уровне за один семестр невозможно. Поэтому в данном курсе я галопом по Европам проскачу лишь по некоторым из основных методов, применяющихся в моделировании плазмы, не углубляясь в те дебри деталей, тонкостей и подробностей, которые человечество успело вырастить вокруг них. Даже то немногое, что здесь излагается, я постарался представить «по рабоче-крестьянски», то есть, стараясь без острой необходимости не выходить за пределы школьного курса математики.
Классификация моделей плазмы
Прежде, чем браться за решение какой-либо задачи, необходимо правильно поставить задачу[2]. Для этого, прежде всего, рекомендуется получить ответ на следующие вопросы:
- Что нужно получить в конечном итоге?
- С какой точностью нужно получить результат?
- Какие ресурсы выделяются на решение задачи?
- Нельзя ли упростить задачу или свести ее к более простым?
Как помочь человеку, который не знает, что ему нужно, рассматривается в других курсах (например, по психологии). В случае четко сформулированной цели дальнейшие действия определяются ответами на вопросы о точности, ресурсах и возможности упрощения задачи.
Ответы на перечисленные выше вопросы, как правило, сводят к минимуму выбор методов, которыми может быть решена поставленная задача. С учетом предельной краткости данного курса, вероятно, несчастный читатель найдет здесь не более одного подходящего для его случая метода. Если известно несколько методов решения задачи, то выбирать следует тот, который привычнее.
Единой общепринятой классификации численных методов не существует, поэтому к приведенным ниже делениям их на классы не следует относиться как к истине в последней инстанции.
Итак, поделим численные методы на эмпирические, полуэмпирические и методы, основанные на решении уравнений, описывающих отдельные процессы [3]. Четкой границы между этими классами не существует.
Эмпирические методы характеризуются тем, что для их реализации вообще не требуется в явном виде какой-либо математической модели процессов, происходящих в моделируемом устройстве. Объект можно считать «черным ящиком». Зависимости между входными и выходными параметрами задаются функциями заранее заданного вида. Коэффициенты в этих функциях подбираются из условия минимизации погрешности, получаемой при подстановке известных экспериментальных данных. Как правило, непосредственно на расчеты уходит времени много меньше, чем на поиск или получение экспериментальной информации. Погрешность зависит от погрешности экспериментальных данных и от того, насколько «близок» рассматриваемый случай к имеющимся в экспериментах. В данном курсе эти методы не рассматриваются. Желающие могут обратиться к книгам [2, 3].
В полуэмпирических методах какая-то математическая модель содержимого «черного ящика» уже появляется, но она предельно упрощена. Требуемую точность при этом пытаются (часто весьма успешно) получить путем введения поправочных коэффициентов, получаемых из экспериментальных данных.
Иногда в качестве математической модели в полуэмпирических методах используется аналитические решения для какой-то более простой задачи. При этом поправочные коэффициенты учитывают различия между реальной задачей и той, для которой построено аналитическое решение. К сожалению, аналитические решения крайне редки.
Полуэмпирические методы сочетают в себе достоинства и недостатки эмпирических методов и методов, основанных на моделировании физических процессов. С одной стороны они требуют минимальное количество ресурсов, с другой – приемлемую точность можно получить только при наличии экспериментальных данных для сходных задач.
Большая часть курса посвящена оставшемуся «безымянному» классу методов. В нем, в свою очередь, тоже можно выделить, по крайней мере, две группы методов (тоже без четкой границы между ними). К первой группе относятся так называемые спектральные методы. В них решение ищется в виде комбинации заранее заданных функций. Эти методы бывают очень эффективными для несложных задач. В другой группе решение ищется в виде сеточных функций, т.е. функций, заданных не непрерывно, а на некотором наборе точек. Т.к. методы этой группы получили наиболее широкое распространение, то им и уделяется основное внимание в данной писанине.
Прежде, чем моделировать какое-либо устройство нужно провести ранжировку процессов. Нужно составить список всех значимых процессов. Обычно составляется сначала список всех процессов, которые потенциально могут оказаться значимыми. Затем проводятся оценки характерных значений физических величин, которые фигурируют в описаниях этих процессов[4]. На основании этих данных оценивают погрешность, которую даст неучет каждого процесса, и сравнивают ее с желаемой погрешностью (см. Вопросы поставленные в начале). По этим данным принимают решение – какие процессы учитывать, а какие нет. Вообще говоря, существуют критерии о включении/не включении процессов в итоговый список. Например,
- сумма погрешностей отброшенных процессов должна быть меньше желаемой погрешности;
- сумма квадратов погрешностей отброшенных процессов должна быть меньше квадрата желаемой погрешности.
На практике, как правило, поступают проще: если оценка погрешности, получающаяся при отбрасывании какого-либо процесса, менее одной десятой от желаемой погрешности, то процесс отбрасывается, иначе – оставляется. Если какой-то процесс решено не учитывать, то полезно сформулировать условие, при котором его необходимо учитывать. Это позволит четко сформулировать область применимости той математической модели, которая будет составлена.
Теперь можно приступить к написанию системы уравнений и граничных и/или начальных условий, а также ограничений. Начнем с конца. Всегда нужно помнить, что математика занимается числами, которые живут самостоятельной жизнью и физикой (в том числе и физикой плазмы) совершенно не интересуются. Поэтому, с точки зрения математики, нет ничего страшного в отрицательных концентрациях и температурах. Если подобные вещи неприемлемы с точки зрения физики, то необходимо либо внести соответствующие ограничения в математическую модель, либо доказать, что в данном случае ничего страшного не произойдет. Обычно, легче поставить ограничения. Но на этом фокусы не кончаются. Сюда же следует включить как ограничения те условия, при которых следует учитывать неучтенные процессы.
При моделировании магнитных полей часто приходится учитывать, что рассчитываемое поле выходит за пределы устройства, в котором оно применяется. Приходится увеличивать расчетную область и ставить условия «на бесконечности». При моделировании плазмы аналогичная ситуация возникает при истечении плазмы в пространство, например, из электроракетного двигателя. Но в большинстве инженерных случаев плазма ограничена стенками устройства или магнитными полями. Часто характерные размеры для процессов, идущих в пристеночных (приграничных) областях, много меньше, чем характерный размер устройства. Это приводит к неприятному факту: если одними уравнениями описывать и процессы, проходящие в объеме плазмы, и процессы, проходящие вблизи границы, то задача становиться совершенно нерешабельной. Эту неприятность обычно обходят, разбивая задачу на две более простые: описание процессов только тех процессов, которые существенны в объеме плазмы, и описание приграничных областей (там, как правило, можно рассмотреть гораздо более простую с точки зрения геометрии задачу). При этом для решения этих двух задач могут использоваться принципиально различные подходы. Часто в объеме рассчитываются уравнения, моделирующие соответствующие процессы, а в качестве граничных условий используются полуэмпирические соотношения.
Для описания процессов в подвижной среде существуют два основных подхода, носящих соответственно имена Лагранжа и Эйлера. В первом уравнения записываются в системе координат, связанной с подвижной частицей (сгустком). Этот подход не получил широкого распространения, однако он используется в некоторых численных методах. Во втором подходе уравнения записываются в инерциальной (как правило, неподвижной) системе координат. Приведем несколько примеров систем уравнений, записанных в рамках подхода Эйлера:
1) Уравнения Максвелла (упрощенная система):
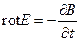
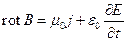
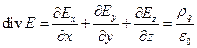
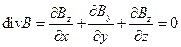
где E – напряженность электрического поля,
rq – объемная плотность зарядов,
j – плотность тока,
B – магнитная индукция.
Эти уравнения в той или иной форме практически всегда входят в физико-математические модели плазмы различных устройств.
2) Уравнения Больцмана
Рассмотрим функцию распределения частиц по пространству и по скоростям. Пусть F(vx, vy, vz, x, y, z, t) – функция, представляющая собой вероятность обнаружения в момент времени t в объеме dV (построенном около точки с координатами x, y, z) частиц со скоростями от v до v+dv. Естественно, если рассмотреть весь возможный диапазон скоростей, то вероятность будет равна 1. То есть

На практике, как правило, пользуются функцией f=nF. При этом
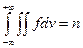
Компоненты осредненной скорости частиц вычисляются по следующим формулам
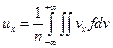
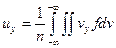

Зная такую функцию распределения можно получить все параметры газа. Эта функция удовлетворяет уравнению Больцмана
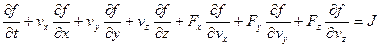
где Fx, Fy, Fz – компоненты силы, действующей на каждую единицу массы частицы (описывают взаимодействие частицы с внешними полями: гравитационным и электромагнитным), J – член, учитывающий столкновение частиц между собой. Даже в простейшем случае член, стоящий в правой части, записывается пятикратным интегралом. Желающие могут посмотреть, например, книги [4, 5]. Решать интегро-дифференциальное уравнение в семимерном (в стационарном случае шестимерном) пространстве – очень дорогое удовольствие. К этому нужно добавить маленькую деталь: такое уравнение нужно решать для каждой из групп частиц (в простейшем случае для электронов, ионов и нейтральных частиц).
Эти уравнения позволяют наиболее полно описать физику процессов в плазме. Но такой подход чрезвычайно требователен к ресурсам. В настоящее время с помощью уравнений Больцмана можно решать лишь самые простые задачи.
3) Магнито-гидродинамическая модель плазмы. Уравнения могут быть получены из законов сохранения, записанных для плотной среды, или из уравнений Больцмана в предположении Максвелловского распределения частиц. В приведенной ниже системе уравнений отсутствуют члены, отвечающие для вязкость, теплопроводность и диффузию, а также переход частиц из одной группы в другую.
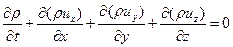
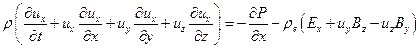
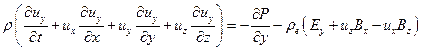
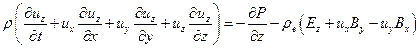
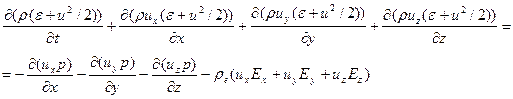
где e - внутренняя энергия
re – плотность заряда.
Первое из этих уравнений представляет собой запись закона сохранения массы. Следующие три уравнения соответствуют закону сохранения импульса (каждое из этих уравнений отвечает за сохранение импульса в одном из трех пространственных направлений). Последнее уравнение представляет собой запись закона сохранения энергии. Левые части этих уравнений отвечают за изменение соответствующего параметра, а правые за причины изменений. В данной записи масса считается неизменной. В случае нескольких групп частиц и учета процессов перехода частиц из одной группы в другую (например, при ионизации) в правой части первого уравнения должен быть записан соответствующий член. В уравнениях сохранения импульса в явном виде написаны члены, отвечающие за силы давления, прочие силы скрываются за значком F.
Контрольный вопрос: почему в правой части уравнения энергии нет членов, зависящих от индукции магнитного поля?
Уравнения магнитной гидродинамики получили широкое распространение за их относительную (по сравнению с уравнениями Больцмана) простоту и «надежность» (они иногда позволяют получить удовлетворительное решение даже за границами своей области применимости). Однако их решение, как правило, требует значительных затрат ресурсов (времени на написание и отладку программ, объем памяти, время счета).
По сути, построение физико-математической модели после прохождения всех перечисленных выше этапов закончено. Но конечной целью, обычно, является не построение модели, а расчет конкретных параметров устройства. Прежде, чем приступить к реализации численного метода, как правило, нужно сделать еще несколько манипуляций.
- Во-первых, нужно посмотреть, нельзя ли воспользоваться еще чем-нибудь для упрощения расчетов. Например, наличие симметрии может в разы сократить объем вычислений.
- Во-вторых, для использования некоторых численных методов полезно записать уравнения какой-либо иной системе координат или в другом виде. Например, для метода конечных разностей желательно иметь так называемую «дивергентную» форму записи уравнений.
- В-третьих, если возможно введение потенциала какой-либо величины (что часто бывает, если можно пренебречь процессами вязкости и теплопроводности), то полезно бывает написать уравнения для потенциала (часто такие уравнения решаются с меньшими затратами ресурсов).
- Далее проверить, нельзя ли разбить задачу на несколько независимых. Например, если магнитное поле, создаваемое токами в плазме, много слабее поля, создаваемого внешней магнитной системой, то его можно рассчитывать независимо от расчета параметров плазмы.
- Наконец, в исследовательских задачах, часто бывает полезным записать уравнения в безразмерном виде. Это позволяет выявить (если до сих пор почему-то не были известны) параметры подобия, лишний раз проверить правильность модели и, в ряде случаев, избавиться от некоторых численных проблем.