
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Analysis
|
|
The traditional theory of electromagnetic acceleration maintains that the actually effective force exerted by an accelerator on an electron is independent of the electron’s speed and all the accelerator’s working energy 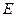 becomes the electron’s kinetic energy
becomes the electron’s kinetic energy 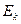 , i.e.,
, i.e., 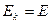 . If the electrons have actually received all the Linac’s working energy (
. If the electrons have actually received all the Linac’s working energy (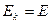 ), then by use of the Einsteinian formula
), then by use of the Einsteinian formula 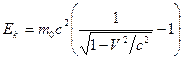 their speeds can be calculated as:
their speeds can be calculated as: 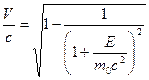 . ( 3.1)
. ( 3.1)
The kinetic energy 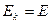 of electrons causes the increase of the lead target’s temperature. The increase of temperature can be calculated as
of electrons causes the increase of the lead target’s temperature. The increase of temperature can be calculated as 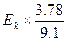 [
[ 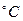 ].
].
Given 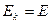 and by use of Einstein’s (3.1), the calculated values of the lead target’s temperature increase are:
and by use of Einstein’s (3.1), the calculated values of the lead target’s temperature increase are:
Linac’s working energy 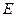 [Mev] [Mev]
| |||||
Calculated speed of electrons 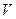
| 0.9969 
| 0.9982 
| 0.9988 
| 0.9992 
| 0.9995 
|
Calculated temperature increase [ 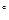 C] C]
| 2.52 | 3.36 | 4.20 | 5.04 | 6.35 |
Table 5
The calculated values of the temperature’s increase in the Table 5 are much bigger than the respective values measured in the Table 4. Moreover, the calculated values vary propotionally to the Linac’s working energy, whereas the measured values vary little. This is because, on the one hand, when the speed of electrons approaches the speed of light, their kinetic energy did not increase as sharply as calculated by use of Eintein’s formula 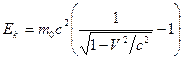 . On the other hand, the Linac’s efficiency decreases sharply as the speed of electrons approaches the speed of light (i.e., the “
. On the other hand, the Linac’s efficiency decreases sharply as the speed of electrons approaches the speed of light (i.e., the “ 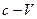 phenomenon” shown in §2) so that the electrons did not reach the speed as high as above calculated in the Table 5.
phenomenon” shown in §2) so that the electrons did not reach the speed as high as above calculated in the Table 5.
Let’s take the “ 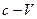 phenomenon” into consideration. An accelerator’s work is to make its electromagnetic field’s potential energy to become the electron’s kinetic energy, i.e., to change the Linac’s potential head into electron’s velocity head:
phenomenon” into consideration. An accelerator’s work is to make its electromagnetic field’s potential energy to become the electron’s kinetic energy, i.e., to change the Linac’s potential head into electron’s velocity head: 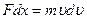 . Due to the quadratic relationship betwee energy and force, an accelerator’s actual work done by its effective force
. Due to the quadratic relationship betwee energy and force, an accelerator’s actual work done by its effective force 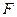 can be expressed as
can be expressed as 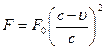 , where
, where 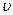 is the electron’s speed and
is the electron’s speed and 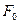 is the accelerator’s nominal force of action. Thus, we have:
is the accelerator’s nominal force of action. Thus, we have:
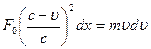 or
or 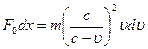 .
.
The nominal work done by an accelerator consuming energy 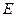 is
is 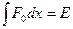 , which accelerates an electron from
, which accelerates an electron from 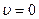 to
to 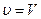 :
: 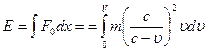 . ( 3.2)
. ( 3.2)
According to the Galilean relativistic mechanics, the formulas of moving mass is 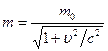 . Placing it into (3.2), we obtain:
. Placing it into (3.2), we obtain:
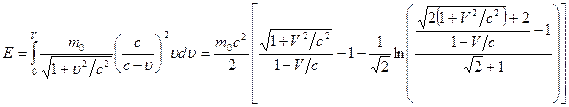 . ( 3.3)
. ( 3.3)
By use of (3.3) we can calculate the actual speed 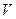 of the electrons accelerated by the Linac’s certain working energy
of the electrons accelerated by the Linac’s certain working energy 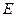 .
.
In the Galilean relativistic mechanics, if a particle moves at speed 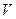 , then its moving mass
, then its moving mass 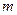 possesses relativistic kinetic energy
possesses relativistic kinetic energy 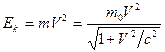 in relation to a static object. Therefore, we can also calculate the lead target’s actual temperature increase as
in relation to a static object. Therefore, we can also calculate the lead target’s actual temperature increase as 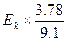 [
[ 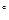 C], the Linac’s wasted energy
C], the Linac’s wasted energy 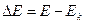 and its efficiency
and its efficiency 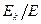 :
:
Linac’s working energy 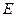 [Mev] [Mev]
| |||||
Calculated speed of electrons 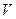
| 0.9488 
| 0.9603 
| 0.9676 
| 0.9726 
| 0.9777 
|
Kinetic energy of electrons 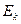
| 0.3337 | 0.3399 | 0.3438 | 0.3442 | 0.3493 |
Calculated temperature increase [ 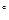 C] C]
| 0.130 | 0.141 | 0.142 | 0.143 | 0.145 |
Linac’s wasted energy 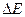 [Mev] [Mev]
| 5.6663 | 7.6601 | 9.6562 | 11.6558 | 14.6507 |
Linac’s efficiency 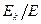
| 5.89% | 4.44% | 3.56% | 2.95% | 2.38% |
Table 6
The calculated values of the lead target’s temperature increase vary little and match the varying trend of the measured values in the Table 4, although not exactly the same values. This is because the electric energy from the discharge of electrons in the lead target may add certain temperature to the target.
Obviously, the Galilean relativistic mechanics together with the consideration of the “ 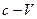 phenomenon” can explain why the lead target’s temperature increases so little.
phenomenon” can explain why the lead target’s temperature increases so little.