
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Analysis. Traditional theory deems that the Lorentz force, which deflects an electron moving in a static homogeneous magnetic field
|
|
Traditional theory deems that the Lorentz force, which deflects an electron moving in a static homogeneous magnetic field, is irrelevant to the electron’s speed 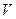 . If the strength of a static homogeneous magnetic field is
. If the strength of a static homogeneous magnetic field is 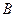 , then the theoretical Lorentz deflecting force is
, then the theoretical Lorentz deflecting force is 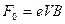 . The Lorentz deflecting force is balanced by the centrifugal force acting on an electron moving circularly due to the deflection. Therefore, the kinematic equation of the electron’s circular motion is:
. The Lorentz deflecting force is balanced by the centrifugal force acting on an electron moving circularly due to the deflection. Therefore, the kinematic equation of the electron’s circular motion is:
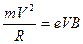 or
or 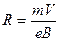 , ( 4.1)
, ( 4.1)
where 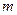 is the electron’s moving mass and
is the electron’s moving mass and  is the radius of the electron’s circular track.
is the radius of the electron’s circular track.
Einstein’s formula 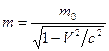 makes the equation (4.1) becoming:
makes the equation (4.1) becoming:
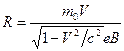 or
or 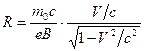 . ( 4.2)
. ( 4.2)
The traditional electromagnetic acceleration theory maintains that all the Linac’s working energy 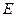 is transferred to the accelerated electron and becomes the electron’s kinetuic energy
is transferred to the accelerated electron and becomes the electron’s kinetuic energy 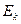 so that
so that 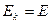 . As above-mentioned in §3.2, the traditional electromagnetic acceleration theory and the Einsteinian relativistic mechanics together lead to the formula (3.1). By use of (3.1) we can calculate the electron’s speed
. As above-mentioned in §3.2, the traditional electromagnetic acceleration theory and the Einsteinian relativistic mechanics together lead to the formula (3.1). By use of (3.1) we can calculate the electron’s speed 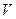 and then by use of (4.2) we can calculate the radius
and then by use of (4.2) we can calculate the radius  of the electron’s circular motion. The calculated values of
of the electron’s circular motion. The calculated values of  are shown below:
are shown below:
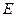 [Mev] [Mev]
| |||||||
| 0.9919 
| 0.9969 
| 0.9986 
| 0.9992 
| 0.9995 
| 0.9997 
| |
| 0.121[tesla] |  [cm] [cm]
| 11.00 | 17.85 | 26.59 | 35.20 | 44.53 | 57.49 |
| 0.081[tesla] |  [cm] [cm]
| 16.43 | 26.66 | 39.72 | 52.58 | 66.52 | 85.88 |
| 0.063[tesla] |  [cm] [cm]
| 21.13 | 34.28 | 51.07 | 67.61 | 85.53 | 110.42 |
Table 8
The calculated value of  increases almost propotionally to the Linac’s working energy level
increases almost propotionally to the Linac’s working energy level 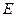 , which does not match the experiment’s results. Thus, both the traditional electromagnetic acceleration theory and the Einsteinian relativistic mechanics are questionable.
, which does not match the experiment’s results. Thus, both the traditional electromagnetic acceleration theory and the Einsteinian relativistic mechanics are questionable.
The above-mentioned calorimetric experiment with high-speed electrons bombarding a lead target has revealed a “ 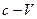 phenomenon” (see §3.2). By use of the formula (3.3), which takes the “
phenomenon” (see §3.2). By use of the formula (3.3), which takes the “ 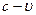 phenomenon” into consideration, we can calculate the speed
phenomenon” into consideration, we can calculate the speed 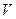 of electrons entering the magnetic field from the Linac. On the other hand, placing
of electrons entering the magnetic field from the Linac. On the other hand, placing 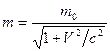 of the Galilean relativistic mechanics into (4.1), we obtain:
of the Galilean relativistic mechanics into (4.1), we obtain: 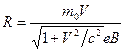 or
or 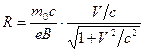 . ( 4.3)
. ( 4.3)
By use of (3.3) and (4.3) we can calculate the electron’s actual speed 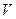 and the radius
and the radius  :
:
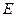 [Mev] [Mev]
| |||||||
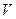
| 0.9299 
| 0.9503 
| 0.9652 
| 0.9730 
| 0.9793 
| 0.9832 
| |
| 0.121[tesla] |  [cm] [cm]
| 0.959 | 0.970 | 0.978 | 0.982 | 0.986 | 0.988 |
| 0.081[tesla] |  [cm] [cm]
| 1.433 | 1.449 | 1.461 | 1.467 | 1.473 | 1.476 |
| 0.063[tesla] |  [cm] [cm]
| 1.842 | 1.863 | 1.878 | 1.886 | 1.894 | 1.898 |
Table 9
The calculated  values in the Table 9 are far smaller than those measured in the experiment. However, the varying trend of
values in the Table 9 are far smaller than those measured in the experiment. However, the varying trend of  values is similar to the vaying trend of
values is similar to the vaying trend of  measured in the experiment.
measured in the experiment.
The Lorentzian deflection is an interaction between a static magnetic field and a moving electron’s moving magnetic field. This is a force-force transaction, not an energy-energy transaction, because the kinetic energy of the electron in circular motion remains constant. Due to the same reason that a sailing-boat can never reach the speed of the wind, we may consider another kind of the “ 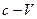 phenomenon” in the action of a static magnetic field’s Lorentzian deflecting force on an electron moving circularly at constant speed
phenomenon” in the action of a static magnetic field’s Lorentzian deflecting force on an electron moving circularly at constant speed 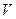 .
.
However, the exact mechanism of this kind of magnetic interaction has not yet been clearly understood and is pending to be studied. We propose to match the theoretically calculated  with the experimentally measured
with the experimentally measured  .
.
In case of 0.121[tesla], the calculated mean value of  is 0.9735[cm] while the experimentally measured mean value of
is 0.9735[cm] while the experimentally measured mean value of  is 18[cm]. The gap is
is 18[cm]. The gap is 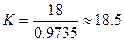 . In case of 0.081[tesla], the calculated mean value of
. In case of 0.081[tesla], the calculated mean value of  is 1.4545[cm] while the measured mean value is 27[cm]. The gap is
is 1.4545[cm] while the measured mean value is 27[cm]. The gap is 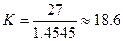 . In case of 0.063[tesla], the calculated mean value of
. In case of 0.063[tesla], the calculated mean value of  is 1.87[cm] while the experimentally measured mean value is 35[cm]. The gap is
is 1.87[cm] while the experimentally measured mean value is 35[cm]. The gap is 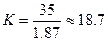 . The matching coefficient
. The matching coefficient 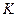 changes very little as the electron’s speed changes from
changes very little as the electron’s speed changes from 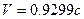 to
to 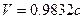 .
.
Therefore, to match the theoretically calculated  with the experimentally measured
with the experimentally measured  values, it is necessary to multiply the calculated values by
values, it is necessary to multiply the calculated values by 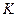 times:
times:
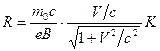 , (4.4)
, (4.4)
where 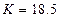 , 18.6 and 18.7 for
, 18.6 and 18.7 for 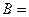 0.121[tesla], 0.081[tesla] and 0.063[tesla] respectively. By use of the formula (4.4) we obtain:
0.121[tesla], 0.081[tesla] and 0.063[tesla] respectively. By use of the formula (4.4) we obtain:
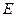 [Mev] [Mev]
| |||||||
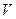
| 0.9299 
| 0.9503 
| 0.9652 
| 0.9730 
| 0.9793 
| 0.9832 
| |
| 0.121[tesla] |  [cm] [cm]
| 17.74 | 17.95 | 18.09 | 18.17 | 18.24 | 18.28 |
| 0.081[tesla] |  [cm] [cm]
| 26.65 | 26.95 | 27.17 | 27.29 | 27.40 | 27.45 |
| 0.063[tesla] |  [cm] [cm]
| 34.07 | 34.47 | 34.74 | 34.90 | 35.03 | 35.11 |
Table 10
The theoretically calculated mean values of  in the Table 10 are 18[cm], 27[cm] and 35[cm] respectively.
in the Table 10 are 18[cm], 27[cm] and 35[cm] respectively.