Вопрос 66

Существуют различные критерии оценки благосостояния. Наибольший прогресс в решении проблемы критериальной оценки благосостояния связывается с именем известного математика и экономиста В. Парето. Работу именно этого автора («Учебник политической экономики», 1906) принято считать водоразделом в истории субъективной теории благосостояния. Так, Парето решительно отошел от традиционной практики, отверг количественную полезность и предложил критерий, никоим образом не зависящий от каких-либо межличностных сравнений полезности.

Суть критерия Парето состоит в том, что любое изменение, которое никому не причиняет убытков и которое приносит некоторым людям пользу (по их собственным оценкам), является улучшением.

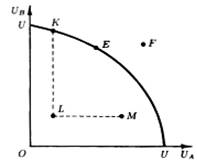
Рисунок 1 – Линия возможных благосостояний

На рисунке 1 представлено благосостояние двух субъектов, А и В, UA и UB. Область, ограниченная кривой UU, представляет все множество возможных благосостоянии двух субъектов, а сама кривая UU называется границей возможных благосостоянии. Ее конфигурация определяется конечными ресурсами этой двухсубъектной экономики, знаниями и применяемой технологией. Понятно, что, как и при рассмотрении границы производственных возможностей, увеличение производственных ресурсов и применяемой технологии сдвигает границу возможных благосостояний вправо вверх. Каждая точка на плоскости UBOUA представляет определенную комбинацию благосостоянии двух субъектов. Очевидно, что комбинация F является недостижимой, так как лежит вне области возможных благосостояний.

Состояние экономики называется Парето-предпочтительным по отношению к другому ее состоянию, если в первом случае благосостояние хотя бы одного субъекта выше, а всех остальных не ниже, чем во втором. Так, на рисунке 1 точки К, Е, М Парето-предпочтительны в отношении точки L. Действительно, в точке К благосостояние субъекта В выше, а субъекта А не ниже, чем в точке L. Напротив, в точке М благосостояние А выше, а В не ниже, чем в точке L. Наконец, в точке Е благосостояние обоих субъектов выше, чем в точке L. С другой стороны, точка К не является Парето-предпочтительной в отношении точки М, поскольку в точке К благосостояние B выше, а благосостояние А ниже, чем в точке М. Соответственно и точка М не является Парето-предпочтительной в отношении точки К, поскольку в ней благосостояние А выше, а В ниже, чем в точке К. Такие состояния экономики называют Парето-несравнимыми. Следовательно, не ко всякой паре точек, характеризующих разные состояния экономики, применимо понятие Парето-предпочтительности. Оно применимо лишь в том случае, если определенную пару точек в пространстве благосостоянии можно соединить отрезком прямой, имеющим неотрицательный наклон (например, KL или LM).

Парето-оптимальным называется такое состояние экономики, при котором невозможно изменить производство и распределение таким образом, чтобы благосостояние одного или нескольких субъектов увеличилось без уменьшения благосостояния других. Как очевидно из рисунка 1, Парето-оптимальные состояния в данной двухсубъектной модели представлены точками К, Е и всеми другими точками, лежащими на границе благосостояний. Переход из одной такой точки в другую обязательно сопряжен с повышением благосостояния одного субъекта и снижением благосостояния другого.

Понятия Парето-оптимальности и Парето-предпочтительности связаны друг с другом. Парето-оптимальное состояние экономики можно определить как такое, по отношению к которому не существует ни одного Парето-предпочтительного. В то же время любая точка, лежащая на границе возможных благосостоянии, например точка К или Е, является Парето-несравнимой в отношении любой другой точки на этой границе. Поэтому можно сказать, что множество Парето-оптимальных состояний есть набор всех Парето-несравнимых состояний, остающийся после исключения из рассмотрения всех нежелательных состояний экономики на основе критерия Парето-предпочтителъности. Действительно, после исключения из рассмотрения всех точек, лежащих внутри области возможных благосостоянии на рисунке 1, у нас останется лишь сама эта граница, UU, все точки которой окажутся Парето-оптимальными относительно точек, лежащих внутри области возможных благосостоянии, но Парето-несравнимыми друг с другом.

Плодотворность использования в экономическом анализе рассмотренных понятий определяется прежде всего тем, что они в явной форме учитывают несовпадение интересов различных субъектов экономики. То, что представляется желательным (хорошим) для одного, может оказаться нежелательным (плохим) для другого. Очевидно, что субъект А сочтет состояние, характеризуемое точкой М, более предпочтительным для себя, чем Парето-оптимальные состояния, представленные точками К или Е. В то же время эти понятия позволяют хотя бы частично упорядочить по предпочтительности все достижимые состояния экономики. И если одна хозяйственная система приводит экономику в состояние, представленное точкой Е, а другая в состояние, характеризуемое точкой L, то бесспорно, что первая система функционирует более эффективно. Поэтому естественным является требование к такой организации экономики, которая приводила бы ее в Парето-оптимальное или, во всяком случае, близкое к нему состояние.

С другой стороны, Парето-оптимальных состояний экономики бесконечно много, на рисунке 1 это все точки, лежащие на границе возможных благосостоянии UU. Какое из них наилучшее (optimumoptimorum)? На этот вопрос экономическая теория не дает однозначного ответа, он относится к сфере общественного выбора (англ, socialchoice). Тем не менее экономическая теория исследует методы перевода экономики из Парето-оптимального, но " социально несправедливого" состояния, такого, например, как то, которое на рисунке отображено точкой К, где UB много выше, чем UA, в более " справедливое", представленное, например, точкой Е, где различия в благосостоянии субъектов А и В не столь разительны, и то, как осуществить такой переход с минимальными потерями в эффективности. [6]