Число размещений из n элементов по m

Пример 4. Различными размещениями из трех элементов {1, 2, 3} по два будут наборы (1, 2), (2, 1), (1, 3), (3, 1), (2, 3), (3, 2). Размещения могут отличаться друг от друга как элементами, так и их порядком.

Число размещений в комбинаторике обозначается A_n^m и вычисляется по формуле:

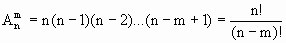
Замечание: n! =1*2*3*...*n (читается: " эн факториал"), кроме того полагают, что 0! =1.

Пример 5. Сколько существует двузначных чисел, в которых цифра десятков и цифра единиц различные и нечетные?

Решение: т.к. нечетных цифр пять, а именно 1, 3, 5, 7, 9, то эта задача сводится к выбору и размещению на две разные позиции двух из пяти различных цифр, т.е. указанных чисел будет:

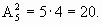
Определение 2. Сочетанием из n элементов по m в комбинаторике называется любой неупорядоченный набор из m различных элементов, выбранных из генеральной совокупности в n элементов.

Пример 6. Для множества {1, 2, 3}сочетаниями являются {1, 2}, {1, 3}, {2, 3}.