
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Прямая, лежащая в плоскости, перпендикулярна наклонной тогда и только тогда, когда она перпендикулярна проекции этой наклонной на данную плоскость.
|
|
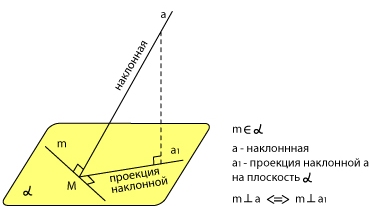
На рисунке показаны все три перпендикуляра.
Если прямая m, лежащая в плоскости, перпендикулярна проекции наклонной, то она перпендикулярна и самой наклонной.
Слова «тогда и только тогда» в формулировке теоремы означают, что прямая m перпендикулярна одновременно и наклонной, и ее проекции. Если m перпендикулярна наклонной, значит, перпендикулярна и ее проекции, и наоборот.
Текст задания:
Задача 1. Прямая АК перпендикулярна к плоскости правильного треугольника АВС, точка М – середина стороны ВС.
1) Докажите, что МК ⊥ ВС
2) Найдите угол между прямой КМ и плоскостью АВС, если АК = а, ВС = 2а.
Задача 2. Из точки М проведен перпендикуляр МВ к плоскости прямоугольника АВСD (рис. 1).
1) Докажите, что треугольники АМD и МСD – прямоугольные.
2) Найдите угол между прямой МD и плоскостью АВС, если СD = 3см,
АD = 4 см, МВ =5 см.
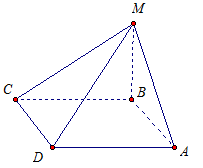
Рис. 1
Задача 3. Катеты прямоугольного треугольника АВ = 8 см и АС = 14 см перпендикулярны прямой АМ, на которой отмечена точка К, так что АК = 4 см. Найдите расстояние от точки К до середины гипотенузы.
Задача 4. К плоскости треугольника АВС, стороны которого АВ = 8 см, АС = 15 см, а угол между ними 120°, проведен перпендикуляр АМ = 42 см. Найдите расстояние от точки М до середины стороны ВС.
Задача 5. В прямоугольном параллелепипеде ABCDA1B1C1D1 укажите углы наклона диагонали B1D к плоскостям граней, имеющих общую вершину В. Вычислите эти углы, если АВ = ВВ1= а, ВС = 2а.
Контрольные вопросы:
[2, стр. 311(9 – 18), 349(4, 5)] [2, стр. 247] [2, стр. 263]
Самостоятельная работа № 15
Тема: Геометрические преобразования в пространстве
Цель: закрепить знания и умения студентов по освоению темы методом решения задач.
Теоритическое обоснование: