
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Формулы и свойства логарифмов
|
|
Логарифмом числа 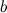 по основанию
по основанию  (
(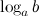 ) называется такое число
) называется такое число  , что
, что  , то есть записи
, то есть записи 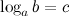 и
и  равносильны. Логарифм имеет смысл, если
равносильны. Логарифм имеет смысл, если  .
.
Если немного перефразировать - Логарифм числа 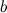 по основанию
по основанию  определяется как показатель степени, в которую надо возвести число
определяется как показатель степени, в которую надо возвести число  , чтобы получить число
, чтобы получить число 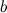 (Логарифм существует только у положительных чисел).
(Логарифм существует только у положительных чисел).
Логарифм в переводе с греческого буквально означает " число, изменяющее отношение".
Специальные обозначения:
1. Натуральный логарифм  - логарифм по основанию
- логарифм по основанию  , где
, где  - число Эйлера.
- число Эйлера.
2. Десятичный логарифм  - логарифм по основанию 10.
- логарифм по основанию 10.
Свойства логарифмов:
1° 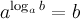 - основное логарифмическое тождество.
- основное логарифмическое тождество.
2° 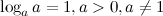
3° 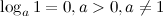
Логарифм единицы по любому положительному, отличному от 1, основанию равен нулю. Это возможно потому, что из любого действительного числа можно получить 1 только возведя его в нулевую степень.
4°  - логарифм произведения.
- логарифм произведения.
Логарифм произведения равен сумме логарифмов сомножителей.
5° 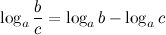 - логарифм частного.
- логарифм частного.
Логарифм частного (дроби) равен разности логарифмов сомножителей.
6° 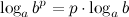 - логарифм степени.
- логарифм степени.
Логарифм степени равен произведению показателя степени на логарифм ее основания.
7° 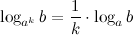
8° 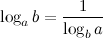
9° 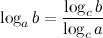 - переход к новому основанию.
- переход к новому основанию.
Текст задания:
Вычислите логарифмы с использованием следующих формул:
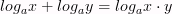 и
и 
1) 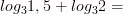
2) 
3) 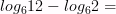
4) 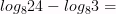
5) 
6) 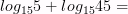
7) 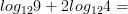
8) 
9) 
10) 
11) 
12) 
13) 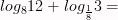
Задачи на основное логарифмическое тождество: 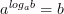
1) 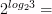
2) 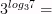
3) 
4) 
5) 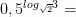
6) 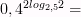
7) 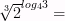
8) 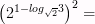
9) 
10) 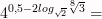
11) 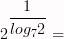
12) 
13) 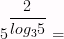
14) 
15) 
16) 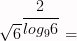
17) 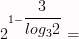
Задачи на формулу перехода к новому основанию 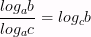
1) 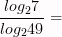
2) 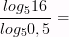
3) 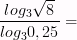
4) 
5) 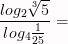
6) 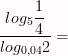
7) 
8) 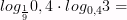
9) 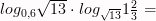
Раздел 3. Основы тригонометрии. Функции, их свойства и графики.
Уравнения и неравенства
Самостоятельная работа № 6
Тема: Формулы половинного аргумента
Цель: закрепить знания и умения студентов применять основные тригонометрические формулы.
Теоритическое обоснование:
Формулы половинного аргумента
1. Синус половинного угла
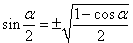
Примечание: Знак перед корнем выбирается в зависимости от квадранта, в который попадает угол α /2 в левой части. Данное правило справедливо также для других формул, приведенных ниже.
2. Косинус половинного угла
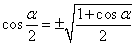
3. Тангенс половинного угла
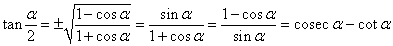
4. Котангенс половинного угла
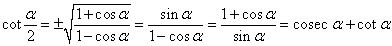
5. Выражение синуса через тангенс половинного угла
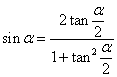
6. Выражение косинуса через тангенс половинного угла

7. Выражение тангенса через тангенс половинного угла
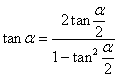
8. Выражение котангенса через тангенс половинного угла
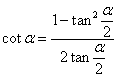
Текст задания:
1. Доказать тождества:
а). 1 + 2 cos 2α + cos 4α = 4 cos2 α cos 2α.
б). 1 — 2 cos 3α + cos 6α = — 4 sin2 3α /2 • cos 3α.
в). 1 + sin α = 2cos2 (π /4 — α /2).
г). 1— sin α = 2sin2 (π /4 — α /2).
2. Упростить выражение 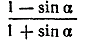
3. Найти sin α, cos α и tg α, если известно, что cos 2α = —0, 6.
4. Найти sin α /2, cos α /2 и tg α /2, если известно, что | cos α | = 0, 6, причем угол α, оканчивается во 2-й четверти,
5. Найти tg α, если sin 2α = 1/3.
6. Вычислить:
а). sin (1/2 arccos 0, 8). в). tg [ 1/2 arcsin (— 0, 8)]
б). cos (1/2 arcsin 0, 6) г). tg [ 1/2 arctg (— 0, 75)]
Самостоятельная работа № 7
Тема: Преобразование тригонометрических выражений
Цель: закрепить знания и умения студентов по освоению свойств тригонометрических функций.
Теоритическое обоснование:

Формулы приведения:


Текст задания:
1. Найти значение выражения  , если известно, что tg α = 1/3
, если известно, что tg α = 1/3
2. Найти значение выражения  , если известно, что котангенс угла α не определен.
, если известно, что котангенс угла α не определен.
3. Найти значение выражения 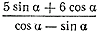 , если известно, что ctg α = ½
, если известно, что ctg α = ½
4. Упростить выражения:
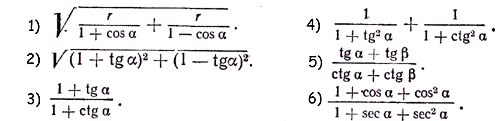
5. Доказать тождества:
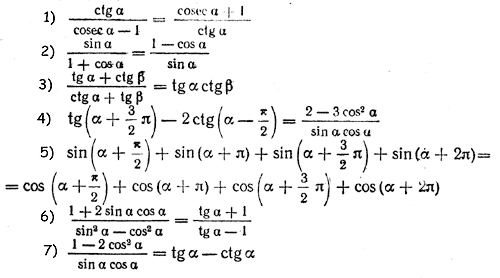
Самостоятельная работа № 8
Тема: Решение тригонометрических неравенств (синус, косинус).
Цель: закрепить знания и умения студентов по освоению методов решения тригонометрических неравенств.
Теоритическое обоснование:
Утверждение 1. Множество решений неравенства sin x > a, есть
- R, если a < -1;
-
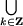 (arcsin a + 2p k; p - arcsin a + 2p k), если -1 ≤ a < 1;
(arcsin a + 2p k; p - arcsin a + 2p k), если -1 ≤ a < 1; - Пустое множество, если a ≥ 1.

Утверждение 2. Множество решений неравенства sin x < a, есть
- R, если a > 1;
-
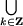 (-p - arcsin a + 2p k; arcsin a + 2p k), если -1 < a ≤ 1;
(-p - arcsin a + 2p k; arcsin a + 2p k), если -1 < a ≤ 1; - Пустое множество, если a ≤ -1.
Утверждение 3. Множество решений неравенства cos x > a, есть
- R, если a < -1;
-
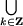 (2p k - arccos a; 2p k + arccos a), если -1 ≤ a < 1;
(2p k - arccos a; 2p k + arccos a), если -1 ≤ a < 1; - Пустое множество, если a ≥ 1.
Утверждение 4. Множество решений неравенства cos x < a, есть
- R, если a > 1;
-
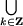 (2p k + arccos a; 2p(k + 1) - arccos a), если -1 < a ≤ 1;
(2p k + arccos a; 2p(k + 1) - arccos a), если -1 < a ≤ 1; - Пустое множество, если a ≤ -1.

Текст задания:
Решить неравенства:
1. sin2 x < cos x.
2. cos x + cos2 x + cos3 x ≥ 0.
3. 6sin2 x - 5sin x + 1 > 0.
4. 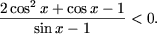
5. 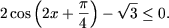
6. 2sin2 x + 9cos x - 6 ≥ 0.
7. 
8. 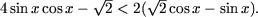
9. cos2 x + sin x ≥ 0.
Самостоятельная работа № 9
Тема: Решение тригонометрических неравенств (тангенс, котангенс).
Цель: закрепить знания и умения студентов по освоению методов решения тригонометрических неравенств.
Теоритическое обоснование:
Утверждение 1. Множество решений неравенства
tg x > a, есть 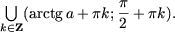
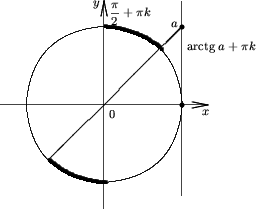
|
Утверждение 2. Множество решений неравенства
tg x < a, есть 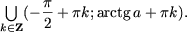
|

Утверждение 3. Множество решений неравенства
ctg x > a, есть 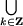 (p k; arcctg a + p k). (p k; arcctg a + p k).
|
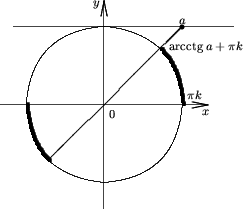
Утверждение 4. Множество решений неравенства
ctg x < a, есть 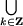 (arcctg a + p k; p(k + 1)) (arcctg a + p k; p(k + 1))
|
Замечания. 1. Если знак неравенства нестрогий, то во множестве решений неравенства включается также и множество решений соответствующего уравнения.
Текст задания:
Решить неравенства:
1. -2 ≤ tgx < 1;
2. 
3. ctg2 x - ctg x - 2 ≤ 0;
4. tg3 x + tg2 x - tg x - 1 > 0.
5. tg x + ctg x ≤ 2.
6. 
Раздел 4. Начала математического анализа
Самостоятельная работа № 10
Тема: Первый и второй замечательный предел
Цель: закрепить знания и умения студентов по вычислению пределов используя первый и второй замечательные пределы.
Теоритическое обоснование:
Первый замечательный предел:

Следствия из первого замечательного предела:
1° 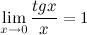
2° 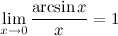
3° 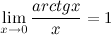
4° 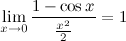
Второй замечательный предел:
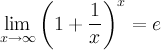
Следствия из второго замечательного предела:
1° 
2° 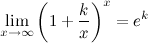
3° 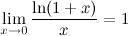
4° 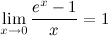
5° 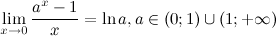
6° 
Текст задания:
Вычислить пределы:
1. 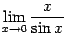 .
.
2. 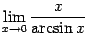 .
.
3. 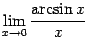 .
.
4. 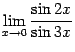 .
.
5.  .
.
6. 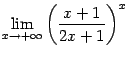
7. 
8. 
9. 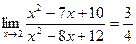
10. 
11. 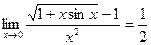
12. 
13. 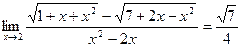
14. 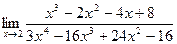 - не определен.
- не определен.
Самостоятельная работа № 11
Тема: Применение производной в прикладных задачах
Цель: закрепить знания и умения студентов по освоению темы, формировать навыки прикладного использования аппарата производной.
Теоритическое обоснование:

Текст задания:
1. Исследуйте функцию y = 1/3x3- 3x2 + 8x и постройте ее график.
2. Исследовать и построить график функции: y = 3x4- 4x3 - 12x2 + 10.
3. Найти ускорение тела, движущегося по закону s (t) = 2 t 3 + 5 t 2 + 4 t (s — путь в метрах, t — время в минутах), в момент времени: a) t = 40 сек; б) t = 1 ч.
4. Найти ускорение тела, движущегося по закону s = √ t (s — путь в метрах, t — время в минутах), в произвольный момент времени t.
5. Для данных функций найти производные всех порядков:
1. у = (х + 2)3. 2. у = х 2 — х — 1. 3. у = cos х.
4. у = (2 х — 1)3. 5. у = х 5+ 4 х 3 — 7 х 2 6. у = (1 + х)100.
6. Доказать, что для функции у = a sin x + b cos х справедливо соотношение y IV= у.
7. Сколько раз нужно продифференцировать функцию у = (х 2 + 1)100, чтобы в результате получился многочлен 50-й степени?
Самостоятельная работа № 12
Тема: Нахождение скорости для процесса, заданного формулой
Цель: закрепить знания и умения студентов по освоению темы, формировать навыки прикладного использования аппарата производной.
Теоритическое обоснование: