
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Гомотетия и подобие пространства
|
|
- Гомотетией пространства с центром O и коэффициентом k ≠ 0 называется преобразование пространства, при котором любая точка М отображается на такую точку М', что
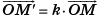 Гомотетию с центром O и коэффициентом k обозначают Hk0
Гомотетию с центром O и коэффициентом k обозначают Hk0
- Подобием пространства с коэффициентом k (k > 0) называется такое преобразование пространства, при котором расстояние между любыми двумя точками изменяется в k раз, то есть для любых двух точек А и В длина отрезка А'B' равна k
 | AB |, где А ' = Рk (A) и B '= Рk (В).Подобие пространства называют также преобразованием подобия. Если при этом подобии фигура F отображается на фигуру F ', то пишут Рk (F)= F' и говорят, что фигура F' подобна фигуре F.
| AB |, где А ' = Рk (A) и B '= Рk (В).Подобие пространства называют также преобразованием подобия. Если при этом подобии фигура F отображается на фигуру F ', то пишут Рk (F)= F' и говорят, что фигура F' подобна фигуре F.
Текст задания:
Задача 1. Можно ли взаимно-однозначно отобразить: а) поверхность куба на поверхность другого куба; б) поверхность куба на сферу; в) сферу с выколотой точкой на плоскость? Сделайте соответствующие рисунки.
Задача 2. Даны точка O и фигура F. Рассмотрим все точки пространства, симметричные точке O относительно всех точек фигуры F. Какую фигуру они образуют, если фигура F:
а) отрезок; б) прямая; в) плоскость; г) треугольник; д) куб; е) шар? Ответ поясните на рисунке.
Задача 3. Даны точки А (3; 2; 1) и В (–1; 2; 6). Найдите координаты образа точки В при композиции центральных симметрий: а) ZА  ZO
ZO
б) ZO  ZA , где точка О — начало координат.
ZA , где точка О — начало координат.
Задача 4. Нарисуйте треугольную пирамиду, имеющую две плоскости симметрии.
Указание. Рассмотрите пирамиду РАВС, в которой лишь АР = ВР = АС = ВС.
Задача 5. В кубе окрашены одним цветом три грани, имеющие общую вершину. Сколько плоскостей симметрии имеет окрашенный таким образом куб?
Задача 6. Точки A и B расположены в одном полупространстве относительно данной плоскости a и не лежат в ней. Постройте в плоскости a такую точку М, сумма расстояний от которой до точек A и B была бы наименьшей.
Задача 7. В основании пирамиды РАВСD лежит квадрат АВСD. Ребро РА пирамиды перпендикулярно ее основанию. Через середину ребра РВ проведено сечение, параллельное плоскости АРD. Какова площадь сечения, если площадь грани АРD равна 48?
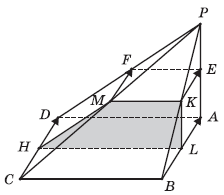 Рис. 1
Рис. 1
Задача 8. Точки D и Е — середины ребер АВ и РС правильного тетраэдра РАВС (рис. 2); точка О — центр грани АВС.
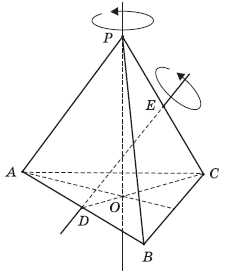
Рис. 2
Задача 9. Докажите, что при вращениях на углы 120°, 240° и 360° вокруг прямой АС 1 куб ABCDA 1 B 1 C 1 D 1 (рис. 3) самосовмещается. Найдите другие вращения, при которых данный куб самосовмещается.
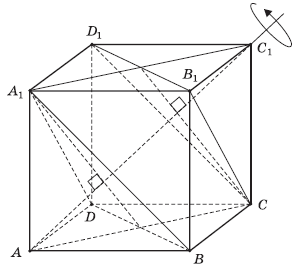
Рис. 3
Задача 10. Постройте тетраэдр, имеющий одну ось симметрии.
Указание. Рассмотрите тетраэдр РАВС, в котором лишь АР = ВР = АС = ВС. Осью симметрии этого тетраэдра служит прямая, проходящая через середины отрезков АВ и РС.
Задача 11. Дан правильный тетраэдр РАВС. Постройте ось симметрии фигуры, являющейся объединением скрещивающихся ребер АР и ВС правильного тетраэдра РАВС.
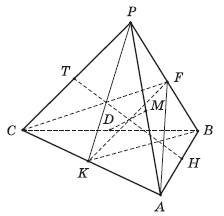
Рис. 4
Задача 12. Дан правильный тетраэдр РАВС; точки Р 1, А 1, В 1, С 1 — центры его граней (рис.5). Докажите, что тетраэдр Р 1 А 1 В 1 С 1 подобен тетраэдру РАВС; найдите коэффициент этого подобия.

Рис. 5
Контрольные вопросы:
[2, стр. 311(19 – 26), 349(2, 3)]
Раздел 6. Многогранники
Самостоятельная работа № 16
Тема: Вписанные правильные многогранники
Цель: закрепить знания и умения студентов по освоению темы методом решения задач.
Теоритическое обоснование:
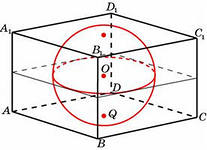
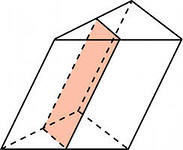

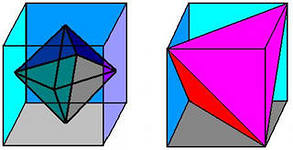
Текст задания:
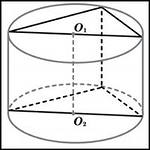
1. В цилиндр высоты 2 вписана сфера. Найдите ее радиус.
2. В цилиндр вписана сфера радиуса 1. Найдите высоту цилиндра.
3. Радиус основания цилиндра равен 2. Какой должна быть высота цилиндра, чтобы в него можно было вписать сферу?
4. Высота цилиндра равна 2. Каким должен быть радиус его основания, чтобы в цилиндр можно было вписать сферу?
5. Периметр осевого сечения цилиндра, в который вписана сфера, равен 8 см. Найдите радиус сферы.
6. Площадь осевого сечения цилиндра, в который вписана сфера, равна 4 см2. Найдите диаметр сферы.
7. Около цилиндра высоты 2 и радиуса основания 1 описана сфера. Найдите ее радиус.
8. Около цилиндра, радиус основания которого равен 1, описана сфера радиуса 2. Найдите высоту цилиндра.
9. Около цилиндра, высота которого равна 1, описана сфера радиуса 1. Найдите радиус основания цилиндра.
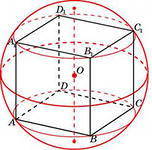
10. Найдите радиус окружности основания цилиндра, вписанного в единичный куб.
11. В основании прямой призмы правильный треугольник со стороной 1. Найдите радиус окружности основания цилиндра, вписанного в эту призму.
12. В основании прямой призмы прямоугольный треугольник с катетами 6 и 8. Найдите радиус окружности основания цилиндра, вписанного в эту призму.
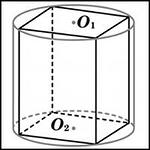
13. В правильную шестиугольную призму, со стороной основания 1, вписан цилиндр. Найдите радиус окружности основания этого цилиндра.
14. В основании прямой призмы квадрат со стороной 1. Найдите радиус окружности основания цилиндра, описанного около этой призмы.
15. В основании прямой призмы правильный треугольник со стороной 1. Найдите радиус окружности основания цилиндра, описанного около этой призмы.
16. В основании прямой призмы прямоугольный треугольник с катетами 6 и 8. Найдите радиус окружности основания цилиндра, описанного около этой призмы.
17. Около правильной шестиугольной призмы, со стороной основания 1, описан цилиндр. Найдите радиус окружности основания этого цилиндра.
18. Около единичного тетраэдра описан цилиндр так, что вершины тетраэдра принадлежат окружностям оснований цилиндра. Найдите радиус основания и высоту цилиндра.
19. В конус, радиус основания которого равен 1, а образующая равна 2, вписана сфера. Найдите ее радиус.
20. В конус, радиус основания которого равен 2, вписана сфера радиуса 1. Найдите высоту конуса.
21. Радиус основания конуса равен 1. Образующая наклонена к плоскости основания под углом 45о. Найдите радиус вписанной сферы.
22. Высота конуса равна 8, образующая 10. Найдите радиус вписанной сферы.
23. В усеченный конус, радиусы оснований которого равны 2 и 1, вписана сфера. Найдите радиус сферы и высоту усеченного конуса.
24. В усеченный конус, радиус одного основания которого равен 2, вписана сфера радиуса 1. Найдите радиус второго основания.
25. В усеченном конусе радиус большего основания равен 2, образующая наклонена к плоскости основания под углом 60о. Найдите радиус вписанной сферы.
26. Около конуса, радиус основания которого равен 1, а образующая равна 2, описана сфера. Найдите ее радиус.
27. Около конуса, радиус основания которого равен 4, описана сфера радиуса 5. Найдите высоту h конуса.
28. Радиус основания конуса равен 1. Образующая наклонена к плоскости основания под углом 45о. Найдите радиус описанной сферы.
29. Высота конуса равна 8, образующая 10. Найдите радиус описанной сферы.
30. Около усеченного конуса, радиусы оснований которого равны 2 и 1, а образующая равна 2, описана сфера. Найдите ее радиус.
1. 1. 2. 2. 3. 4. 4. 1. 5. 1. 6. 2. 7. 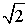 . 8.
. 8. 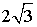 . 9.
. 9.  . 10. 0, 5. 11.
. 10. 0, 5. 11. 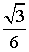 . 12. 2. 13.
. 12. 2. 13.  . 14.
. 14. 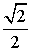 . 15.
. 15. 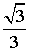 . 16. 5. 17. 1. 18.
. 16. 5. 17. 1. 18. 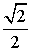 . 19.
. 19. 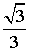 . 20.
. 20.  . 21.
. 21.  . 22. 3. 23.
. 22. 3. 23. 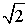 . 24. 0, 5. 25.
. 24. 0, 5. 25. 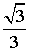 . 26.
. 26. 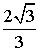 . 27. 8. 28. 1. 29. 6, 25. 30. 2.
. 27. 8. 28. 1. 29. 6, 25. 30. 2.
Контрольные вопросы:
[2, стр. 333(1 – 5), 360(1, 7)]
Раздел 7. Тела и поверхности вращения