
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Кольорові сітки Петрі
|
|
Кольорові сітки Петрі є однією з найбільш важливих модифікацій традиційних сіток Петрі. За їх допомогою вдається досить компактно моделювати складні системи з великим числом різних динамічних об’єктів.
До таких систем, зокрема, відносяться багатономенклатурні багатоверстатні гнучкі виробництва.
Кольорова сітка Петрі (КСП) формально визначається як набір виду:
N = (P, Т, W, F, Н, l, y, m0),
де Р = { р } – непорожня кінцева множина позицій;
Т = { t } – непорожня кінцева множина переходів;
W = {w} – непорожня кінцева множина кольорів маркерів;
F: P ´ T ® {0, 1, 2,...} і Н: Т ´ Р ® {0, 1, 2,...} – функції інцидентності множин позицій і переходів відповідно;
l: (Р ´ W) ´ Т ® (0, 1) – функція розподілу кольорів маркерів по вхідних позиціях переходів сітки;
y: T ´ (P ´ W) ® (P ´ W) – функція розподілу кольорів маркерів по вихідних позиціях переходів сітки;
m0: (P ´ W) ® {0, 1, 2,...} – початкове маркування сітки.
Функція l довизначає умови збудження, а y - правило спрацьовування переходів, внаслідок чого здійснюється розподіл кольорів маркерів по позиціях сіткі при її функціонуванні.
Умова збудження переходу t Î T при деякому маркуванні m має вид:
 (3.1)
(3.1)
Для кожного t Î T, що задовольняє умові (3.1), у загальному випадку функція l t визначає множину допустимих вхідних розподілів кольорів маркерів, при яких ця умова виконується
 .
.
Функція y t для кожного допустимого вхідного розподілу з 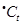 ставить у відповідність єдиний допустимий вихідний розподіл кольорів маркерів з множини
ставить у відповідність єдиний допустимий вихідний розподіл кольорів маркерів з множини
 ,
,
тобто визначає результат спрацьовування переходу і правило формування нового маркування сітки
 .
.
Тоді умова спрацьовування переходу t, збудженого при вхідному розподілі кольорів маркерів 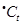 , в наслідок чого буде утворено нове марування, має вид:
, в наслідок чого буде утворено нове марування, має вид:

На рис. 3.8 представлений приклад графічного зображення КСП для двох кольорів: w1 і w2 (позначені відповідно «*» і «·»).
Функції l і y для даної сітки представлені нижче:
для t 1: для t 2: для t 3:
l t 1((p 1, w1)) = 1; l t 2((p 2, w1)) = 0; l t 3((p 3, w1), (p 1, w1)) = 0;
l t 1((p 1, w2)) = 0; l t 2((p 2, w2)) = 1; l t 3((p 3, w2), (p 1, w2)) = 1;
l t 3((p 3, w1), (p 1, w2)) = 1;
l t 3((p 3, w2), (p 1, w1)) = 0;
y t 1(p 1, w1) = (p 2, w2); y t 2(p 2, w2) = (p 3, w1); y t 3((p 3, w2), (p 1, w2)) = (p 2, w1);
y t 3((p 3, w1), (p 1, w2)) = (p 2, w1).

Рис. 3.8. Графічне зображення КСП
Виділимо два окремих види КСП: перероджуючі (ПС) і селективні (СС) сітки.
У перероджуючих сітках (ПС) спрацьовування будь-якого переходу t дозволене за наявності у всіх вхідних позиціях p Î • t маркерів одного кольору w j Î W. Після спрацьовування даного переходу в усіх його вихідних позиціях містяться маркери іншого кольору w g Î W.
Функція l у ПС задається наступним чином:

де  – допустимий вхідний розподіл виду:
– допустимий вхідний розподіл виду:
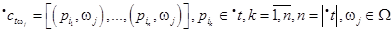
Функція  у ПС набуває значень з області допустимих вихідних розподілів:
у ПС набуває значень з області допустимих вихідних розподілів:
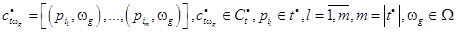
Якщо 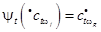 , то перехід t при спрацьовуванні перероджує маркери кольору w j у вхідних позиціях в маркери кольору w g у вихідних позиціях.
, то перехід t при спрацьовуванні перероджує маркери кольору w j у вхідних позиціях в маркери кольору w g у вихідних позиціях.
Умова збудження переходу t Î T при вхідному розподілі 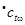 маркування m для ПС записується у виді:
маркування m для ПС записується у виді:
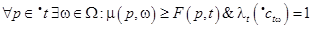 (3.2)
(3.2)
Нове маркування m¢, одержане в результаті спрацьовування переходу t при вхідному розподілі 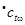 , визначається за правилом:
, визначається за правилом:

Приклад ПС з W = {w1, w2, w3, w4} показаний на рис. 3.9. Початкове маркування m0 і функція y описуються матрицями (табл. 3.1, 3.2).
Таблиця 3.1 Таблиця 3.2
| m0 | Кольори | y | Кольори | ||||||||
| w1 | w2 | w3 | w4 | w1 | w2 | w3 | w4 | ||||
| Позиції | p 1 | Переходи | t 1 | w2 | w 3 | w1 | w2 | ||||
| p 2 | t 2 | w4 | w1 | w2 | w3 | ||||||
| p 3 | t 3 | w4 | w4 | w3 | w2 | ||||||
| t 4 | w1 | w1 | w4 | w1 |
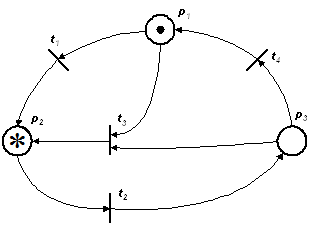
Рис. 3.9. Графічне зображення ПС
Селективною сіткою (СС) називається така сітка, у якій переходи пропускають тільки маркери певних кольорів, не змінюючи їх.
Функція l t для СС задається так само, як і для ПС, а функція  .
.
Умови збудження переходу t Î T СС і ПС при маркуванні mаналогічні (3.2). Нове маркування m ¢ при спрацьовуванні переходу t Î T по розподілу 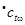 визначається за правилом:
визначається за правилом:

Приклад СС для двох кольорів w1 і w2 (позначені «·» і «*») зображений на рис. 3.10. Функція l представлена матрицею (табл. 3.3).
Таблиця 3.3
| l | Кольори | ||
| w1 | w2 | ||
| Переходи | t 1 | ||
| t 2 | |||
| t 3 | |||
| t 4 | |||
| t 5 |

Рис. 3.10. Графічне зображення СС
Отже, у СС множину переходів T можна розбити на підмножини Тi, де " t Î Ti пропускає маркер кольору w i. При цьому  .
.
Підсіткою СС, що визначена на множині переходів Тi Í Т, називається така сітка Петрі Ni = (Pi, Ti, Fi, Нi, m i 0), у якій:
 ;
;
 ;
;
 ;
;
 .
.
Кожна підсітка Ni, є одноколірною сіткою з маркерами кольору w i.
Отже, аналіз СС можна звести до аналізу сукупності одноколірних сіток.
Властивості КСП. Розглянемо властивості обмеженості, безпеки, зберігаємості та живучості КСП.
Обмеженість та безпека. Будемо розрізняти безпеку та обмеженість КСП у цілому і по кожному визначеному кольору w Î W. Назвемо позицію р Î Р k-обмеженою по кольору w Î W, якщо існує k Î {0, 1,...} таке, що на множині всіх досяжних маркувань m(p, w) £ k.
Сітка Петрі є k-обмеженою по кольору w, якщо всі її позиції k-обмежені по кольору.
Позиція р Î Р називається k-обмеженою, якщо існує k Î {0, 1,...} таке, що на множині всіх досяжних маркувань " w Î W, m(p, w) £ k.
Сітка Петрі називається k-обмеженою, якщо всі її позиції k-обмежені. Окремим випадком k-обмеженості сітки в цілому й обмеженості її по кольору w Î W є безпека і безпека по кольору w (випадок k = 1).
Очевидно, що якщо сітка з різнокольоровими маркерами ki обмежена по кожному кольору w i, то вона k-обмежена, де 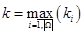 . Вірно і зворотнє: якщо сітка з різнокольоровими маркерами k-обмежена, то вона k-обмежена по будь-якому кольору w i Î W.
. Вірно і зворотнє: якщо сітка з різнокольоровими маркерами k-обмежена, то вона k-обмежена по будь-якому кольору w i Î W.
Аналіз обмеженості сітки Петрі з різнокольоровими маркерами аналогічний аналізу обмеженості звичайної сітки.
Збереженість. У КСП виділимо збереженістьсітки в цілому і по окремих кольорах.
КСП є збереженою по кольору w j, якщо існує вектор l= (l1, l2,..., l n), l i > 0 такий, що для всіх маркувань m(p, w j), досяжних з початкового m0(p, w j), справедлива рівність:
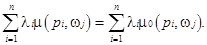
Сітка Петрі з різнокольоровими маркерами називається збереженою, якщо існує вектор l = (l1, l2,..., l n), l i > 0, такий, що для кожного маркування m(p, w), " р Î Р, " wÎ W, досяжного з початкової сітки, справедлива рівність:

Якщо КСП є збереженою по будь-якому кольору w Î W, то вона є збереженою в цілому.
Живучість. КСП N назвемо живою, якщо:
1) " t Î T $m i, m j досяжні з початкового маркування m0 такі, що 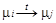 (тобто маркування m j досяжне з m i);
(тобто маркування m j досяжне з m i);
2) " m i, m j досяжні з початкового маркування 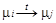 ;
;
3) " w Î W $m досяжне з початкової КСП таке, що $ р Î Р, m(p, w) ¹ 0.
Селективна сітка N є живою по кольору w i, якщо сітка Ni, яка є фрагментом селективної сітки N і визначена на множині переходів Тi, жива.
Графи досяжності сіток Ni є підграфами графа досяжності СС N при m0 i (p) =m0(p, w i). При цьому маркування m i, m j, що належать графу досяжності СС, будуть належати графу досяжності Gi сітки Ni тоді і тільки тоді, коли:
m i (p, w l) = m j (p, w l); m i (p, w i) ¹ m j (p, w i),  ; t ¹ i.
; t ¹ i.
Отже, селективна сітка N жива тоді і тільки тоді, коли кожна Ni,  , жива.
, жива.
Перероджуюча сітка, наведена на рис. 3.9, не є живою. Селективна сітка, показана на рис. 3.10, також не є живою, оскільки сітки N 1, N 2 неживі.
Відзначимо, що КСП із кінцевим числом кольорів маркерів еквівалентна звичайній сітці Петрі з точки зору можливостей відображення властивостей об’єкта моделювання. Однак використання КСП дозволяє значно скоротити кількість позицій і переходів, необхідних для опису об’єкта, що значно спрощує і прискорює процес моделювання.
Практика моделювання показує, що незважаючи на теоретичну можливість, часто не вдається через велику розмірність та складність побудувати звичайну сітку Петрі для таких об’єктів, як дільниці ГВС із значною кількіст‘ю технологічного і транспортного устаткування. Використання ж КСП істотно спрощує цю задачу моделювання.
Оцінимо збільшення обсягу даних, необхідного для опису об’єкта сіткою при переході від КСП до еквівалентної їй звичайній сітці Петрі.
Нехай для КСП ï P ï = n; ï T ï = m; ï Wï = r. Тоді F – матриця розмірності n ´ т, Н – матриця розмірності т ´ n, m – матриця розмірності n ´ r.
Обсяг даних (число елементів) для опису КСП визначається виразом 2 mn + nr.
Щоб у сітці Петрі зберегти таку ж кількість станів, як і в еквівалентній їй КСП, необхідно кожній позиції КСП поставити у відповідність r позицій звичайній сітці. Очевидно, при цьому число переходів також збільшиться не менше, ніж у r разів. Отже, обсяг даних для її опису можна оцінити виразом 2 nmr 2 + nr.
Таким чином, оцінкою зміни обсягу даних може служити відношення:
 .
.
Очевидно, що при r = 1 значення g = 1. Для будь-якого m величина g оцінюється знизу виразом 2 r 2/(2 + r). Це означає, що при перетворенні КСП в еквівалентну їй звичайну сіику Петрі обсяг даних зростає не менше, ніж у 2 r 2/(2 + r) разів.
Відмітимо, що при m ® ¥ величина g ® r 2, тобто при досить великій розмірності для опису КСП потрібно в r 2 разів менше пам’яті, ніж для опису еквівалентної їй звичайній сітці Петрі.