
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Дослідження матричного подання сітки Петрі
|
|
Побудова і аналіз дерева досяжності потребує встановлення усіх досяжних у сітці маркувань, що є важкою задачею повного перебору станів. Тому існує інший спосіб, який представляє собою структурний аналіз сітки, що базується на матриці інциденцій та початкового маркування.
Виходячи з умови збудження та правила спрацьовування переходів, динаміку сітки в просторі станів (маркувань) можна описати рекурентним рівнянням – рівнянням стану сітки:
Mk = Mk –1 + A • Uk; k = 1, 2,..., (3.3)
де Mk – стан, у який перейде сітка зі стану m k -1 у результаті k -го впливу Uk (спрацьовування переходу);
Uk = [ Ujk ] – керуючий вектор, компонента якого Ujk = 1, якщо в k -й момент асинхронного часу виникає спрацьовування переходу tj, або Ujk = 0, якщо спрацьовування не відбувається;
A = [ Aij ] – матриця інциденцій позицій та переходів, елементи якої визначаються наступним чином: Aіj = l, якщо перехід tj має l вихідних дуг до позиції pі, Aіj = - l, якщо перехід tj має l вхідних дуг з позиції pі, Aіj = 0, якщо перехід tj немає зв’язку з позицією pі.
Матрицю А можна розрахувати на підставі операції над матрицями F = [ Fij ] і H = [ Hij ], які задають кількість дуг, що виходять відповідно з позицій і переходів:
A = H – F,
тобто елементи Fіj задають кількість маркерів, які потрібно забрати з позиції pі при спрацьовуванні переходу tj, а елементи Hіj визначають кількість маркерів, які направляються у позицію pі при спрацьовуванні переходу tj.
Очевидно, що в будь-якому стані компоненти вектора маркування не можуть бути від’ємними. Вони можуть набувати лише нульових або додатних цілочисельних значень. Ця умова у матричному записі має вигляд: Mk ³ 0 для всіх k. Враховуючи останнє, з рівняння станів одержуємо Mk –1 + A • Uk ³ 0, а послідовність маркувань (3.3) можна замінити єдиним виразом через початкове маркування M 0 і вектор підрахунку спрацьовувань переходів сітки:
 . (3.4)
. (3.4)
Елемент sj вказує, яку кількість разів спрацьовує перехід tj в послідовності маркувань, яка йде від M 0 до Mk. Враховуючи рівняння (3.4), з (3.3) одержимо:
Mk = M 0 + A • S, (3.5)
або якщо додати вектор зміни маркірування
dM = Mk – M 0,
з рівняння (3.5) одержимо рівняння:
A • S = dM. (3.6)
Всі можливі рішення даного рівняння можна отримати за допомогою одного з методів розв’язку задач цілочисельного програмування.
Розглянемо використання методів лінійної алгебри у розв’язанні рекурентних рівнянь зміни станів моделі сітки. Вони дозволяють на основі математичного дослідження структури біграфа сітки і початкового маркування M 0оцінити такі якісні характеристики сітки, як обмеженість, живучість.
Цілочисельний вектор  , який є розв’язком лінійної системи
, який є розв’язком лінійної системи
AT • X = 0 (3.7)
називається р - інваріантом.
Розглянемо рівняння (3.3), обидві частини якого помножимо на транспонований вектор XT:
XT • M = XT • M 0 + XT • A • S. (3.8)
Враховуючи (3.7) i те, що AT • X = ХT • А, з виразу (3.8) одержимо:
XT • M = XT • M 0, (3.9)
тобто будь-який p -iнварiант характеризує всi досяжнi маркування сітки з точки зору збереження деяких властивостей процесiв, що моделюються сіткою.
Якщо позначити
XT • M = К 0,
де К 0 – константа,
то iнварiантнiсть досяжних маркувань сітки представимо у виглядi спiввiдношення:
XT • M = К 0 = const. (3.10)
Вектор X тому називають p -інваріантом, що він визначає властивості структури сітки у розподілі маркерів за позиціями pі незалежно від будь-якого досяжного маркування.
Враховуючи, що система (3.7) може мати нескінченну кількість рішень, фундаментальною системою розв’язків системи лінійних однорідних рівнянь називають таку сукупність розв’язків, за допомогою якої виражаються всі інші розв’язки.
Якщо ранг матриці A дорівнює числу невідомих (r = n), то система (3.7) має тільки нульовий розв’язків. Якщо r < n, то система (3.7), крім нульового, має нескінченну множину інших розв’язків, причому фундаментальна (базисна) система складається з (n – r) векторів p -інваріант.
Ранг матриці A = [ aij ] розміром n ´ m дорівнює найвищому порядку відмінного від нуля визначника, одержаного викреслюванням (n – r) стовпців і (m – r) рядків з матриці A. Таким чином, всі інваріанти X для маркувань сітки можна отримати з (n – r) базисних рішень, тобто  , де
, де 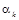 - коефіцієнт лінійної комбінації векторів базисних рішень
- коефіцієнт лінійної комбінації векторів базисних рішень  . Об’єднавши записані у вигляді векторів-рядків розв’язки фундаментальної системи, одержимо матрицю інваріантів чи базисних розв’язків
. Об’єднавши записані у вигляді векторів-рядків розв’язки фундаментальної системи, одержимо матрицю інваріантів чи базисних розв’язків 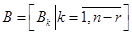 .
.
Тоді подібно до (3.9) для будь-якого досяжного маркування будемо мати:
B • M = B • M 0 = K 0. (3.11)
Якщо всі компоненти p -інваріанта невід’ємні, його називають p- ланцюгом.
Повний p -ланцюг – це p -інваріант, всі компоненти якого додатні, тобто повний p- ланцюг включає всі позиції сітки.
Сітка Петрі інваріантна, якщо для неї існує повний p-ланцюг. Повний p -ланцюг потрібно шукати серед усіх рішень фундаментальної системи В або їх лінійної комбінації.
Інваріантна сітка Петрі є обмеженою, але обмежена сітка може не бути інваріантною, тобто не мати повного ланцюга. Це випливає з того, що якщо X – повний p -ланцюг і XT • M = K 0, то зважена сума маркерів за всіма позиціями 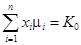 є обмеженою. А оскільки xі – додатні і вся сума обмежена, то і маркування m і всіх позицій сітки обмежені. Необхідно зауважити, що якщо повний p -ланцюг є одиничним вектором, то сітка є безпечною.
є обмеженою. А оскільки xі – додатні і вся сума обмежена, то і маркування m і всіх позицій сітки обмежені. Необхідно зауважити, що якщо повний p -ланцюг є одиничним вектором, то сітка є безпечною.
Розглянемо наступну характеристику сітки – живучість, визначення якої базується на обчисленні t -інваріантів.
Цілочислений вектор  називається t - інваріантом, якщо він є розв’язком лінійної однорідної системи:
називається t - інваріантом, якщо він є розв’язком лінійної однорідної системи:
A • Y = 0. (3.12)
Якщо значення t -інваріанта підставити в рівняння (3.5) замість вектора підрахунку спрацьовувань переходів S, то виявиться, що
M = M 0 + A • Y = M 0.
Звідси випливає, що якщо Y ¹ 0, то сітка стійка, тобто після деяких спрацьовувань переходів вона повертається в початковий стан M 0. Стійкість сітки пов’язана з її циклічною повторюваністю, починаючи зі стану M 0. Необхідно зазначити, що серед розв’язків системи (3.12) можуть бути і такі вектори Y, компоненти яких від’ємні.
Повний t -ланцюг – це t -інваріант, всі компоненти якого додатні. Повний t -ланцюг включає усі переходи сітки. Якщо сітка має повний t -ланцюг, то вона стійка, що є тільки необхідною умовою живучості при будь-якому початковому маркуванні, оскільки встановлено, що в послідовності маркувань від m0 до m = m 0 спрацьовують всі переходи, але не визначено чи існують тупикові маркування. Пошук повного t -ланцюга здійснюється подібно до пошуку повного p -ланцюга.
Тобто, якщо ранг матриці A дорівнює числу невідомих (r = m), то система (3.12) має тільки нульовий розв’язків. Якщо r < m, то система (3.12), крім нульового, має нескінченну множину інших розв’язків, причому фундаментальна (базисна) система складається з (m – r) векторів t -інваріант.
Таким чином, якщо сітка жива і обмежена, то вона стійка і інваріантна. Тому для остаточного вирішення задачі аналізу на живучість потрібно перевірити сітку на досяжність тупикових станів.
Тупик – це досяжний з початкового маркування стан, у якому не збуджений жоден з переходів сітки.
Запишемо умову збудження переходу tj у наступному вигляді:
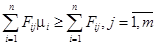
або
F • M ³ F • E,
де E – одиничний вектор.
Оскільки множина досягаємих маркувань R (N) повинна задовольняти умові (3.11), то відсутність збуджуваних переходів для m Î R (N) необхідно визначити з розв’язку системи
 (3.13)
(3.13)
Якщо ця система має розв’язок M, то деяке її маркування є тупиковим, в іншому випадку сітка немає тупиків і є живою.