Методи аналізу модифікацій сіток Петрі

Для кольорових сіток існують аналогічні методи аналізу властивостей роботи, що розглядалися у попередніх пунктах.

Наведемо тільки відмінності у застосуванні, що існують для методу аналізу матричного подання при знаходженні інваріант кольорової сітки [11].

Динаміку руху маркерів у кольоровій сітці записують рівнянням:

M_k = M_{k +1} + D • U_k,

де 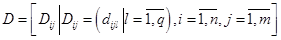– тривимірна матриця, елементи якої D_ij подаються у вигляді векторів-рядків розмірністю q. Якщо позиція p_i має вихідні дуги кольору c_l до переходу t_j, то d_ijl = -1, якщо позиція p_i має вхідні дуги кольору c_l з переходу t_j, то d_ijl = 1, якщо немає дуг цього кольору, то d_ijl = 0, тобто матриця D формується на базі функцій F i H із врахуванням функцій l і y.

Властивості сітки встановлюють наступним чином. Для визначення обмеженості розв’язують систему:

D^T • V = 0,

де V = [ V_i ] – вектор-стовпець p -інваріанти, компоненти якого подаються як .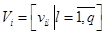

Фундаментальна система B має (n – rq) розв’язків, якщо r – ранг матриці D, n – кількість позицій, q – кількість кольорів маркерів.

Для визначення живучьості розв’язують систему:

D • W = 0,

де W = [ W_j ] – вектор-стовпець t -інваріанти, компоненти якого подаються як .

Умова існування тупиків в кольоровій сітці знаходиться з аналізу системи:

B • M = B • M ₀;

O • M £ O • E ¢ – E,

де 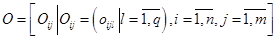; o_ijl = 1, якщо існує дуга кольору c_l з p_i в t_j;

E ¢ = [ E_j ] – вектор, компоненти якого подані наборами з q одиниць.