
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задания для самостоятельного выполнения
|
|
1. Задайте множество А перечислением его элементов:
| 0)A={xÎ R|(x2–6x+5)× (x2–x–12)=0} | 1)A={xÎ R |(x2–5x+6)× (x2+x–0)=0} |
| 2)A={xÎ R|(x2 –5x +4)× (x2–x–6)=0} | 3)A={xÎ R|(x2+4x–5)× (x2–x+12)=0} |
| 4)A={xÎ R| (x2+3x–4)× (x2+x–12)=0} | 5)A={xÎ R |(x2–5x–6)× (x2–x–6)=0} |
| 6)A={xÎ R |(x2 +x–2)× (x2–7x+6)=0} | 7)A={xÎ R|(x2–3x–4)× (x2–9x+20)=0} |
| 8)A={xÎ R |(x2–3x+2)× (x2–4x–5)=0} | 9)A={xÎ R |(x2–x–2)× (x2–x–20)=0} |

2. Заданы множества: А = {1, 3, 9, 10, 8}, B = {5, 3, 11, 4, 8}
и C = {1, 4, 8, 9, 10}. Найдите элементы множеств Д и Е:
| 0)Д = Аî þ Вì ü С; Е = (А D В) | С; | 1)Д = (Аî þ С) | (Вì ü С); Е = А| Вì ü С; |
| 2)Д = Аî þ Вî þ С; Е = Аì ü С D В; | 3)Д = (Аî þ С)ì ü В; Е = А DВî þ С; |
| 4)Д = (Аî þ С) | В; Е = (В D С) | А; | 5)Д = Аì ü Вì ü С; Е = С D В | А; |
| 6)Д = Аî þ (В D С); Е = А | В | С; | 7)Д = (Вî þ С)|(Аì ü С); Е = Аî þ В | С; |
| 8)Д = (Аî þ В)ì ü С; Е = А D В | С; | 9)Д = (Аî þ В) D С; Е = Аì ü В | С; |

3. Изобразите с помощью диаграмм Эйлера-Венна в двух вариантах расположения следующие множества:
0) а)U½ 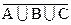 ;
б) ;
б) 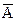 ì ü B½ C; ì ü B½ C;
| 1)а)Cî þ А½ 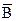 ;
б)(А½ В)î þ C; ;
б)(А½ В)î þ C;
| 2)а) (AD В)½ C;
б) 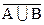 ì ü С; ì ü С;
|
| 3)а)Аì ü В½ С; б)Aì ü Вî þ С½ А; | 4)а) 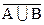 ½ С;
б)(В½ А)ì ü C; ½ С;
б)(В½ А)ì ü C;
| 5)а) 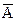 ì ü ì ü 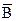 ½ С;
б) ½ С;
б) 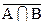 ½ С; ½ С;
|
6)а)С½ Аî þ В;
б)  ì ü (ВD С); ì ü (ВD С);
| 7)а)U½  ;
б)Cì ü А½ ;
б)Cì ü А½  ; ;
| 8)а)A½ (BD C); б)С½ Аì ü В; |
| 9) а) (Аî þ В)ì ü (ВD С); б)Aî þ В½ C; |
а)
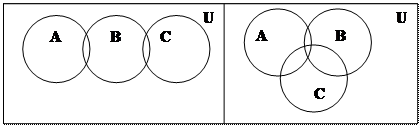
б)
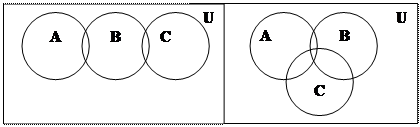 |
Законы теории множеств
| Аî þ В | º Вî þ А; | Aî þ Æ | º А; |
| Аì ü В | º Вì ü А; | Aì ü Æ | º Æ; |
| Аî þ (Вî þ С) | º (Аî þ В)î þ С; | Aì ü 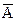
| º Æ; |
| Аì ü (Вì ü С) | º (Аì ü В)ì ü С; | Aî þ A | º А; |
| Аì ü (Вî þ С) | º (Аì ü В)î þ (Аì ü С); | Aì ü A | º А; |
| Аî þ (Вì ü С) | º (Аî þ В)ì ü (Аî þ С); | 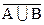
| º 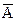 ì ü ì ü 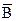 ; ;
|
| Аî þ U | º U; | 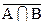
| º 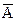 î þ î þ 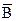 ; ;
|
| Aì ü U | º А; | Aî þ (Aì ü B) | º А; |
Aî þ 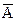
| º U; | Aì ü (Aî þ B) | º А |
Равносильности теории множеств
| А½ В | º Аì ü 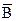 ; ;
| A½ (В½ С) | º (А½ В)î þ (Aì ü С); |
| А½ А | º Æ; | (A½ В)½ С | º A½ Bî þ С; |
| А½ (Вî þ С) | º (А½ В)ì ü (A½ С); | AD В | º BDA; |
| А½ (Вì ü С) | º (А½ В)î þ (A½ С); | AD В | º Аî þ В ½ Аì ü В; |
| (Аì ü В)½ С | º (А½ С)ì ü (В½ С); | AD В | º (А½ В)î þ (В½ А); |
| (Аî þ В)½ С | º (А½ С)î þ (В½ С); | AD(ВD C) | º (AD В)D C; |
| А½ (А½ В) | º Aì ü B; | Аì ü (ВDC) | º (Аì ü В)D(Aì ü C). |
4. Докажите тождества:
0)X ∪ 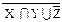 º Z ∪ X º Z ∪ X
 º º  ∩ ∩ 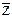 X ∩
X ∩ 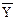 ∪ Z | ∪ Z | 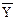 º Z | º Z | 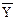 Y | (
Y | (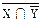 ∪ Z) º Æ; ∪ Z) º Æ;
| 1)X ∩ Y∩ (X∩ Z∪ X∩ Y∩ Z∪ Z∩ t) º X ∩ Y∩ Z
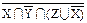 º Y∪ º Y∪  ∪ ∪ 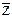 (X | (X |
(X | (X | 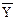 )) ∪ ( )) ∪ ( | ( | ( | | 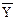 ))º ))º 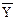
 ∩ ( ∩ (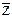 | X ∪ | X ∪ 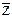 ) º Æ; ) º Æ;
|
2)  ∩ Y∩ Z∪ X∩ Zº (X∪ Y) ∩ Z
X∪ ∩ Y∩ Z∪ X∩ Zº (X∪ Y) ∩ Z
X∪ 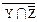 ∪ ∪ 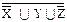 º X∪ Z∪ º X∪ Z∪ 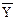 Y | (Y | X∪
Y | (Y | X∪ 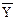 ) º Y ∩ X
( ) º Y ∩ X
(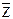 ∩ ∩  | X) | | X) | 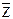 º Æ; º Æ;
| 3)X ∩ Y∪ X∩ Y∩ Z∪ X∩ Y∩ Z∪ X∩ Y∩ Zº X∩ Y
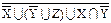 º X ∩ º X ∩ 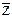 ∩ Y
(X | ∩ Y
(X |  ) | ) | 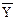 º X
(X ∩ º X
(X ∩ 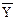 ) | ( ) | ( ∪ ∪ 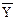 ) º Æ; ) º Æ;
|
4)  ∪ Y ∩ Z ∪ ∪ Y ∩ Z ∪ 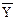 ∪ ∪  ∪ ∪ 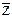 º U º U
 ∩ ∩ 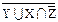 º º 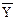 ∩ ∩ 
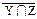 | | 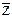 º Z | Y º Z | Y
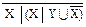 º Æ; º Æ;
| 5) ((X∪ Y) ∪ ( ∩ ∩ 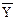 )) ∩ )) ∩  º X ∩ º X ∩ 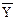
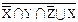 º ( º (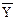 ∪ Z) ∩ ∪ Z) ∩  X | Y∪ X ∩ Zº X | Y ∩
X | Y∪ X ∩ Zº X | Y ∩ 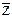
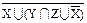 º Æ; º Æ;
|
6) 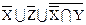 º U º U
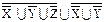 º X ∩ Y º X ∩ Y
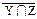 | |  º X ∩ º X ∩ 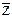 ∩ Y ∩ Y
 ∩ (Y ∪ Z) ∩ X ∩ Y º Æ; ∩ (Y ∪ Z) ∩ X ∩ Y º Æ;
| 7) (X∪ Y∪ Z) ∩ (X∪ Y) ∪ Zº X∪ Z∪ Y
 º º  ∪ ∪ 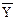 Y | (X ∩ Y |
Y | (X ∩ Y | 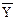 ) º Y | X ) º Y | X
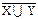 | |  ∪ Y º Æ; ∪ Y º Æ;
|
8)X ∪ 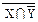 ∪ X ∩ Z º U ∪ X ∩ Z º U
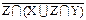 ∪ ∪  º º  ∪ ∪ 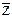 X ∪
X ∪ 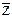 ∩ (Y| ∩ (Y|  ) º X ) º X
 | |  ∪ ∪ 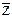 º Æ; º Æ;
| 9) (X∪ Z) ∩ (X∪ Y) ∩ (Y ∩ Z) º Y ∩ Z
 ∩ ∩ 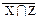 º (Y∪ º (Y∪ 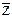 ) ∩ ) ∩  (
(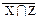 | | 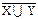 ) | ) |  º X | Z º X | Z
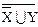 ∩ ∩  º Æ; º Æ;
|
Практическое занятие №2.
Графы
Любая система, предполагающая наличие дискретных состояний или наличие узлов и переходов между ними может быть описана графом. Связи между узлами(вершинами) (V), определенные неупорядоченными парами вершин графа, называются ребрами (E), а граф –неориентированным. Если пары вершинупорядочены, связи называются дугами
(рис. 2).
| Пара вершин может быть соединена двумя или более ребрами (дугами), такие ребра (дуги) называются кратными. Вершины, соединенные ребром (дугой) называются смежными. Если ребро начинается и заканчивается в одной и той же вершине, то называется петлей. |  Рис. 2. Примеры А) неориентированного и Б) ориентированного графов.
Рис. 2. Примеры А) неориентированного и Б) ориентированного графов.
|