Рівняння стану ідеального газу. Теплоємність ідеального газу.

Стан заданої маси визначається значеннями трьох макропараметрів: тиску р, об’єму V і температури Т. Зазначений зв'язок може бути заданий аналітично у вигляді функції 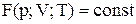. Співвідношення, що визначає зв'язок між параметрами p, V і Т, називається рівнянням стану. Найпростішими властивостями володіє газ, взаємодією між молекулами в якому зневажають. Такий газ називають ідеальним. Рівняння стану ідеального газу має вигляд:

.

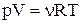Це рівняння називають рівнянням Менделєєва–Клапейрона. n – кількість речовини, що вимірюється в молях. Моль – міра виміру речовини кількістю частинок. В одному молі будь–якої речовини вміщується стільки ж частинок, скільки їх знаходиться у вуглеці масою 0, 012 кг. Це число називають числом Авогадро:

.

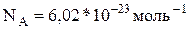R – універсальна газова стала:

.

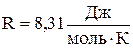Маса одного моля речовини називається молярною масою:

.

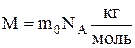Теплоємністю тіла називають фізичну величину, яка дорівнює кількості теплоти, яка необхідна тілу для нагрівання на 1 К:

, .

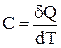Теплоємність одного моля речовини називається молярною теплоємністю:

, .

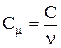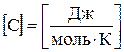Теплоємність одиниці маси речовини називають питомою теплоємністю:

, .

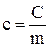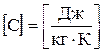Між молярною і питомою теплоємністями існує зв'язок: .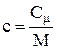

Теплоємність є функцією процесу, оскільки вона залежить від вигляду процесу, при якому систему переводять з одного стану в інший.

Ізопроцесом називають процес переходу газу з одного стану в інший при одному фіксованому макропараметрі. Процес, при якому об’єм газу залишається сталим, називається ізохоричним. З рівняння Менделєєва–Клапейрона випливає, що при незмінній кількості речовини 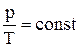– закон Шарля: При постійному об’ємі відношення тиску до абсолютної температури є величиною сталою. Робота газу при ізохоричному процесі дорівнює нулю, оскільки dV = 0. Тоді математичне вираження першого закону термодинаміки приймає вигляд:

.

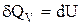Для одного моля газу

,

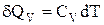де 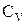– молярна теплоємність газу при постійному об’ємі.

Після відповідної підстановки вираження для зміни внутрішньої енергії приймає вигляд:

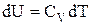
і

,

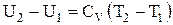відкіля одержуємо формулу внутрішньої енергії, як функцію температури:

.

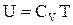Для довільної маси газу остання формула приймає вигляд:

.

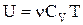Процес переходу газу з одного стану в інший при постійному тиску називається ізобаричним. З рівняння стану ідеального газу випливає:

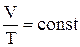– закон Гей–Люссака: при постійному тиску відношення об’єму до абсолютної температури є величиною постійною.

Математичне вираження першого закону термодинаміки для ізобаричного процесу має вигляд:

.

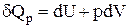Розділивши ліву і праву частини останньої рівності на dТ одержимо:

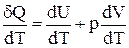
або

,

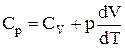де 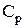– молярна теплоємність газу при постійному тиску.

Рівняння стану одного моля ідеального газу має вигляд:

.

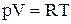Продифференціював останнє рівняння з урахуванням сталості тиску, отримуємо:

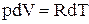
або

.

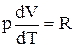З останнього вираження випливає, що робота одного моля ідеального газу при ізобаричному нагріванні його на 1 К дорівнює універсальної газової сталої. Після відповідної підстановки формула молярної теплоємності при постійному тиску здобуває вигляд:

.

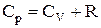Отримане рівняння називається рівнянням Майєра.

Важливою характеристикою газів є відношення 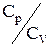, що позначається буквою g і називається постійною адіабати. З урахуванням рівняння Майєра можна записати:

,

відкіля одержуємо формулу для молярної теплоємності при постійному об’ємі:

.

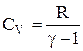Підставивши отриману формулу у вираження для внутрішньої енергії, одержуємо:

.

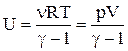Ізотермічним називають процес переходу газу з одного стану в інше при сталій температурі. З рівняння Менделєєва–Клапейрона випливає закон Бойля-Маріотта: 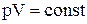– при незмінній температурі добуток тиску на об’єм є величиною сталою. Оскільки Т = const, то внутрішня енергія системи не змінюється (dU = 0), і математичний вираз першого закону термодинаміки приймає вигляд:

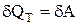
і

.

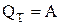Визначимо роботу газу при ізотермічному розширенні:

.

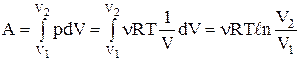Таким чином, для збільшення об’єму газу від V₁ до V₂ при сталій температурі необхідно системі передати кількість теплоти:

Адіабатичним називається процес, що протікає без теплообміну з навколишнім середовищем. Оскільки 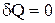, то перший закон термодинаміки для адіабатичного процесу буде мати вигляд:

.

Але 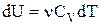, а 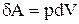. Після підстановки одержуємо:

.

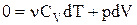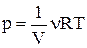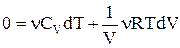Оскільки , то або .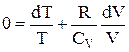

Останнє вираження являє собою диференціал суми логарифмів:

,

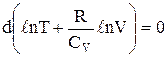відкіля випливає що .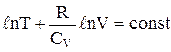

Враховуючи, щ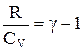о , то 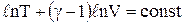. Використовуючи властивості логарифмів (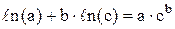), одержуємо:

.

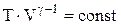Виразимо температуру з рівняння Менделєєва–Клапейрона і підставимо в останню формулу:

, .

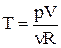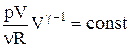Але, оскільки 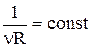, то в остаточному підсумку одержуємо:

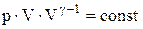
або

.

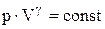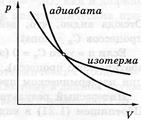
Отримане рівняння називається рівнянням Пуассона. Слід зазначити, що в природі в реальних умовах не існує ідеально ізольованих систем. Однак кількість теплоти, яким обмінюється система з навколишнім середовищем буде тим менше, чим менше часу триває процес. Тому близькими до адіабатичного є тільки процеси, які протікають дуже швидко. Графік адіабатичного процесу – адіабата. Зіставлення рівняння ізотерми 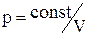з рівнянням адіабати 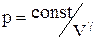з урахуванням того, що g > 1, дозволяє зробити висновок, що адіабата йде крутіше, ніж ізотерма, тобто адіабатне розширення газу супроводжується його охолодженням.

Політропічним називається процес переходу газу з одного стану в інше, при якому теплоємність залишається сталою (С_n = const). Рівняння залежності тиску від об’єму при політропічному процесі має вигляд:

,

де n – довільне число.

Оскільки 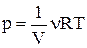, то після підстановки одержуємо:

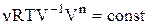або .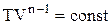

Отримане рівняння є рівнянням політропи в системі TV. Покажемо, що при політропічному процесі теплоємність газу залишається сталою. Математичний запис першого початку термодинаміки має вигляд:

.

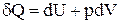Розділимо ліву і праву частину на dТ:

.

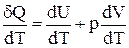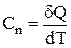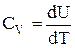З огляду на те, що і , одержуємо:

.

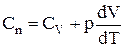Оскільки 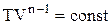, то похідна від лівої частини дорівнює нулю:

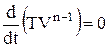, і ,

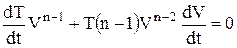відкіля випливає:

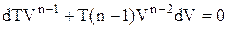
або

.

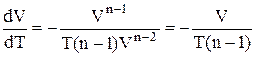Для одного моля газу 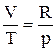. Після підстановки одержуємо:

.

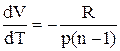Підставимо останнє вираження у формулу теплоємності:

.

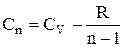З огляду на те, що 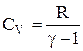, остаточно одержуємо:

,

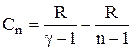відкіля випливає, що теплоємність речовини при політропічному процесі є величиною сталою.

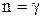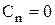Якщо , то і 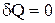, тобто одержуємо адіабатичний процес. При 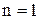одержуємо 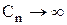і Т = const, тобто ізотермічний процес.

Визначимо роботу газу при політропічному процесі. З першого початку термодинаміки випливає:

.

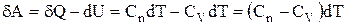Для n молів газу

.

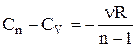Тому вираження для роботи можна переписати у вигляді:

.

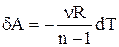Повна робота дорівнює:

.
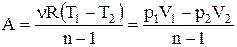