
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Дати означення закону та багатокутника розподілу ймовірностей д.в.в. Навести приклади.
|
|
Законом розподілу дискретної випадкової величини називають таке співвідношення, яке встановлює зв’язок між можливими значеннями випадкової величини і відповідними їм ймовірностями; його можна задати таблично, аналітично (у вигляді формули).
Для наочності закон розподілу дискретної випадкової величини можна зобразити і графічно, для чого в прямокутній системі координат будують точки (хі, рі), а потім з’єднують їх відрізками прямих. Отриману фігуру називають багатокутником розподілу.
Задати закон розподілу д.в.в. — це задати рівність рk=Р(Х=хk), яку можна розглядати як функцію. Функція розподілу для дискретної випадкової величини має вигляд
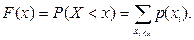
Наприклад, умовами лотереї передбачено: 1 виграш—100 грн., 2—50 грн., 8—10 грн., 19—1 грн. Знайти закон розподілу суми виграшу власником одного лотерейного білету, якщо продано 1000 білетів. Будемо шукати закон розподілу у вигляді ряду розподілу.
| Х | |||||
| Р(Х) | 0.001 | 0.002 | 0.008 | 0.019 | 0.97 |
Де р(0)=1-(0.001+0.002+0.008+0.019)=1-0.03=0.97
Це табличний спосіб задання функції.
А, якщо задавати графічно, то треба взяти прямокутну систему координат. На осі асцис будемо відкладати можливі значення ДВВ, а на осі ординат — відповідні значення імовірності. Одержимо точки з координатами (х1, р1), (х2, р2), …, (хn, pn).
 Р
Р
р3
р4
P2
P1
Р5
Поєднавши ці точки прямими, одержимо графік у вигляді многокутника розподілу випадкової дискретної величини.