Друга форма нерівності Чебишова.

Якщо випадкова величина Х має скінчені математичне сподівання та дисперсію, то для довільного ε > 0 має місце нерівність

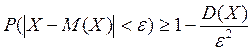
Сформулювати основні теореми закону великих чисел: а) Бернуллі; б) Чебишова; в) Центральну граничну теорему. Пояснити зміст букв.

Теорема Бернуллі:

Нехай імовірність появи події А в кожному із n незалежних повторних випробувань дорівнює р, m – число появ подій А (частота події) в n випробуваннях. Тоді

.

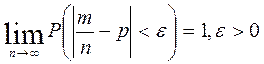Теорема Чебишова:

Нехай Х₁, Х₂, …, Х_n – попарно незалежних випадкових величин, які задовольняють умовам

1)М(Х_і)= а_і, 2) D(Х_і)≤ с для усіх і= 1, 2, …, n. Тоді

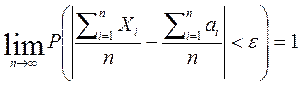
Центральна гранична теорема.:

Нехай задана послідовність незалежних однаково розподілених випадкових величин Х₁, Х₂, …, Х_n, М(Х_і)=0, D(Х_і)= b, і= 1, 2, ….

Розглянемо випадкову величину Y_n= 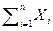. Тоді

М(Y_n)= ,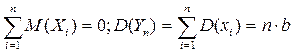

При 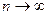функція розподілу

,

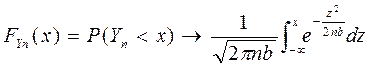Тобто сума Y_n буде розподілена за нормальним законом з математичним сподіванням 0 та дисперсією