Дати означення а) інтегральної; б) диференціальної функції розподілу н.в.в. Вказати їх основні властивості. Навести приклади.

Інтегральною функцією розподілу називають імовірність того, що випадкова величина Х прийме значення, менше х. Функцію розподілу позначають F(x). Таким чином,

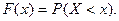
Якщо НВВ Х може приймати будь-яке значення з (a, b), то ,

тобто імовірність прийняття величиною Х значень з (a, b) дорівнює приросту функції розподілу.

Властивості інтегральної функції:

1)

2) 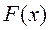— зростаюча функція, тобто 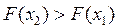, якщо ;

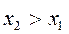3)

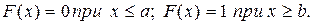
Диференціальною функцією розподілу або щільністю імовірностей неперервної випадкової величини називають похідну першого порядку від її інтегральної іункції розподілу і позначають .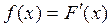

Властивості диференціальної функції:

1) 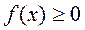, тому, що вона є похідною зростаючої функції ;

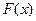2) 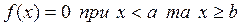тому, що є похідною ;

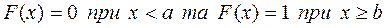3) 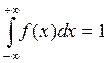тому, що подія 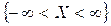— достовірна.

Дати означення основних числових характеристик в.в.: а) математичного сподівання; б) дисперсії; в) початкового та центрального моментів; г) асиметрії; д) ексцесу; е) моди; ж) медіани. Записати формулу для їх обчислення для д.в.в. та н.в.в.. Пояснити зміст букв, навести приклади.

Математичним сподівання Х називають число, яке дорівнює сумі добутків можливих значень Х на відповідні їм імовірності.

М(Х) або m_X —математичне сподівання ДВВ.

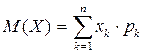
Якщо Х приймає нескінченну кількість значень, то

.

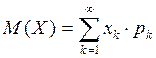Математичне сподівання для НВВ обчислюється за формулою

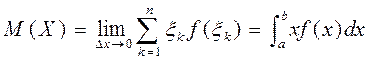
Де ;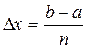

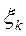—певне значення Х;

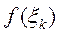— імовірність того, що Х приймає значення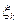

Дисперсія Х — це число, яке дорівнює математичному сподіванню квадрата відхилення в.в. від її математичного сподівання.

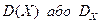— дисперсія величини Х.

Обчислення дисперсії для ДВВ:

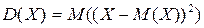
Обчислення дисперсії для НВВ:

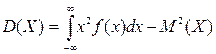
Початковим моментом порядку k в.в. Х називають математичне сподівання величини Х^k і позначають 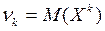, k=1, 2, …, n.

Центральним моментом порядку k в.в. Х називають математичне сподівання величини 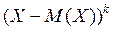і позначають 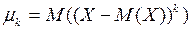k=1, 2, …, n.

Асиметрією або коефіцієнтом асиметрії називається величина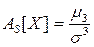

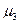— центральний момент 3-го порядку

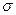— середнє квадратичне відхилення

Якщо A_S=0 (A_S 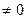), то розподіл симетричний (асиметричний);

Якщо A_S> 0 (A_S< 0), то асиметрія правостороння (лівостороння).

Ексцес в.в. характеризує плоско- чи гостроверхість розподілу, порівняно з нормативним розподілом з тим же значенням дисперсії.

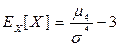. Якщо Е_Х> 0 (Е_Х< 0), то розподіл гостроверхий (плосеоверхий).

При графічному способі зображення закону розподілу в.в., значення в.в. імовірність якого найбільша, називають модою (М₀).

Медіана (Ме)— це середина відрізку між математичним сподіванням та модою.