
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Записати ф-ли для обчислення ймовірностей попадання випадкової точки в довільну двомірну область D; в прямокутник.
|
|
· Імовірність влучення випадквої точки (Х, У) в довільну облась D знаходять: P((X, Y,)єD)=∫ ∫ df(х, у)dxdy
Р- ймовірність влучення точки;
f(х, у)- щільність розподілу
· Імовірність влучення випадкової точки до прямокутника { x1 ≤ Х ≤ х2; у1 ≤ У≤ у2}можна знайти за формулою: Р(x1 < Х < х2; у1 < У< у2)= {F(х2, у2)- F(х1, у2)}- {F(х2, у1)- F(х1, у1)}
х, у – координати точки в просторі
F(х, у)-ф-ція розподілу.
36. Дві випадкові величини наз. незалежними, якщо закон розподілу кожної з них не залежить від того, які ймовірні значення прийняла інша величина. Отже, умовні розподіли незалажних величин дорівнюють їхнім умовним розподілам. Теорема: для того щоб випадкові величини X і Y були незалежними, необхідно і достатньо, щоб функція розподілу системи (X, Y) дорівнювала добутку функцій розподілу складових:
Необхідно: F (x, y) = F1(x) F2(y).
Достотньо: нехай F(x, y) = F1(x) F2(y). Звідси P(X< x, Y< y) = P(X < x) P (Y< y).
Звідси для того щоб неперервні випадкові величини X і Y були незалежними, необхідно і достатньо, щоб щільність спільного розподілу системи (X, Y) дорівнювала добутку щільностей розподілу складових: f (x, y) = f1(x)f2 (y). Достатньо F (x, y) = F1(x) F2(y).
37. Функцією розподілу ймовірностей С.В.В. наз. така функція двох змінних F (x, y), що її значення в кожній в.в. точці дорівнює F (x, y) = P(X< x; Y< y)
Функція щільності розподілу наз. другу змішану похідну від функцію розподілу: f (x, y) = 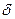 2 F (x, y)/
2 F (x, y)/ 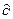 x
x 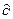 y.
y.
38. Умовним розподілом складових X при Y= yj називають сукупність умовних ймовірностей p (x1| yj), p (x2| yj) … p (xn| yj), обчислених при умові, що подія Y=yj (J має одне і те саме значення при всіх значеннях X) вже настала. Аналогічно і для Y.
Закон розподілу для X:
P (xi| yj) = p (xi, yj) / p (yj).
P (yj| xi) = p (xi, yj) / p (xi).
39. Умовною щільністю (x|y) розподілу складових X при даному значенні Y = y називають відношення щільності спільного розподілу f(x, y) системи (X, Y) до щільності розподілу f2(y) складової Y:
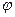 (x|y) = f(x, y)/ f2 (y)
(x|y) = f(x, y)/ f2 (y)
Аналогічно визначається умовна щільність складової Y при даному значенні X= x:
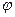 (y| x) = f(x, y)/ f1(x).
(y| x) = f(x, y)/ f1(x).
40. Математичне сподівання двохвимірної випадкової величини (X, У)характеризує координати центру розподілувипадкової величини. Ці координати у випадку неперервних величин знаходять за формулами:
MX = 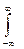
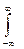 x f(x, y) dx dy; MY =
x f(x, y) dx dy; MY = 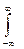
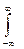 y f(x, y) dx d
y f(x, y) dx d  y.
y.
Дисперсії Dх та Dухарактеризують розсіювання випадкової точки (X, У)вздовж координатних осей Ох та Оу, відповідно. їх знаходять за формулами:
DX = 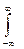
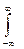 x2 f(x, y) dx dy – m2X ; DY =
x2 f(x, y) dx dy – m2X ; DY = 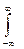
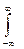 y2 f(x, y) dx dy – m2Y ;
y2 f(x, y) dx dy – m2Y ;
Для опису двохвимірної випадкової величини крім математичного сподівання, дисперсії та середніх квадратичних відхилень використовують також
інші характеристики, а саме- кореляційний момент(або коваріація)
cov (X, Y) = KXY = M ((X – mx) (Y – my)).
Для неперервних величин Xта У
KXY = 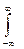
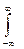 (x - mx) (Y – my) f (x, y) dx dy.
(x - mx) (Y – my) f (x, y) dx dy.
Коефіцієнт кореляціїy
r XY = KX  Y/
Y/ 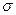 x
x 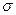 y
y
Коефіцієнт кореляції є кількісна характеристика залежності випадкових величин X та У і часто використовується в статистиці.
41. Навести основні властивості кореляційного моменту μ xy та коефіцієнту кореляції rxy
Корреляционный момент млужит для х-ки связи между величинами X и Y. КМ равен нулю, если X и Y независимы; следовательно, если КМ не равен нулю, то X и Y – зависимые случайные величины.
Величина коэф. корреляции не зависит от выбора единицы измерения случайных величин. В этом состоит преимущество коэф. корреляции перед корреляционным моментом. КК независимых сл. величин равен нулю (так как μ xy = 0).
Абсолютная величина кор. момента двух случайных величин X, Y не превышает среднего геометрического их дисперсий: 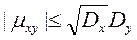
Абсолютная величина коэф. кореляции не превышает единицы.
Властивості кор.моменту μ xy:
1) Кор.момент 2 незалежних в.в. Х та Y=0; І навпаки, якщо кор.момент не равен 0, то Х та Y – залежні в.в.
2) Абсолютна величина кор.моменту 2 в.в. Х та Y не перевищує середнього геометричного їх дисперсій: | 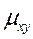 |< =
|< = 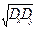
Властивості коефіцієнта кореляції:
1) | rxy| < = 1; 2) Якщо Х та Y незалежні, то rxy= 0; 3) Якщо між Х та Y є лінійна залежність Y=a*X+b, де a та b – сталі, то | rxy |=1
Корельованими наз.2 в.в., якщо їх μ xy відрізняється від 0.
Некорельваними наз. 2 в.в., якщо їх μ xy =0