Дати означення корельованості (некорельованості) двох в.в. Пояснити різнцю і зв’язок між корельованістю (некорельованістю) і залежністю двох в.в.

Две случайные величины X и Y называют коррелированными, если их корреляционный момент (или, что то же, коэффициент корреляцыии) отличен от нуля; X и Y называют некоррелированными величинами, если их корреляционный момент равен нулю. Две коррелированные величины также и зависимы. Действительно, допустив противное, мы должны заключить, что μ _xy = 0, а это противоречит условию, так как для коррелированных величин μ _xy не равняется 0. Обратное предположение не всегда имеет место, т.е. если две величины зависимы, то они могут быть как коррелированными, так и некоррелированными. Другими словами, корреляционный момент двух зависимых величин может быть не равен нулю, но может и равнятся нулю. Для нормально распределенных составляющих двумерной случайной величины понятия независимости и некоррелированности равносильны.

Зв’язок між корел-тю(некорел-тю) та залежністю:

1) якщо Х, Y некорельовані μ _xy =0, то залежність невідома.

2) якщо Х, Y корельовані, то вони залежні

3) якщо X, Y незалежні, то вони некорельовані X, Y =0

4) якщо X, Y залежні, то вони можуть бути як корельованими так і некорельованими

μ _xy – індикатор залежності і незалежності X, Y

Різниця: із незалежності 2 величин слідує їх некорельованість, але із некорельваності неможна зробити висновок о незалежності цих величин.

Вивести рівняння лінійної середньоквадратичної регресії Y на Х(Х на Y). Пояснити зміст позначень.Дати означення коефіцієнту регресії, залишкової дисперсії та пояснити, що вони характеризують.

Лінійна середньоквадратична регресія Y на Х має вигляд

g(X)=m_y+ 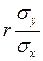(X – m_x), де m_x=М(Х), m_y=М(Y), σ _x= 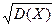, σ _y= , r=μ _xy/(σ _xσ _y) – коефіцієнт кореляції величин Х та Y.

Виведення:

Введем у розгляд функцію двох незалежних аргументів 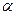та :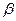

F(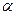, 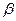)=M[Y - 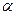- 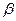X]^2. (*)

Враховуючи, що М(Х – m_x)=M(Y – m_y)=0,

M[(X - m_x)*(Y - m_y)]= μ _xy=r σ _xσ _y та виконав викладки, отримаємо

F(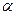, 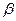)= + 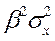- 2r σ _xσ _y 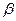+(m_y - 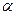- 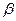m_x)²

Дослідим функцію F(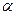, 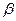) на екстремум, для чого прирівняєм 0 часткові похідні:

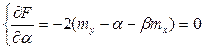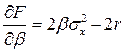, σ _xσ _y=0

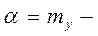
Звідси , 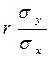m_x

Легко впевнитися, що при цих значеннях 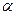та 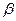розглянута функція приймає найменше значення. Звідси лінійна середньоквадратична регресія Y та X має вигляд

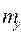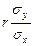g (X)= X= - m_x+ 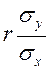X, або g(X)=m_y+ 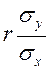(X – m_x),

Коефіцієнт 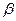= наз. коефіцієнтом регресії Y на X

Підставимо знайдені значення 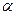та 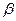у співвідношення (*), отримаємо мінімальне значення значення функції F(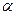, 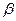), яке дорівнює 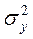(1 – r²). Величину 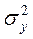(1 – r²) наз. залишковою дисперсією в.в. Y відносно в.в. Х..Вона характеризує величину похибки, яку допускають при заміні Y лінійної функції g(X)= 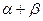X. При r=⁺ -1 залишкова дисперсія =0

Аналогічно можно отримати пряму середньоквадратичної регресії Х на Y

X - m_x=r (Y- m_y), де r - коефіцієнт регресії Х на Y.Залишкова дисперсія 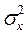(1-r²) величини Х відносно Y.