Кривые второго порядка

1 Линии на плоскости: основные понятия, определения, классификация

Пусть на плоскости задана прямоугольная декартова система координат Оху и некоторая линия L, заданная уравнением (1):

, (1)

т.е. кривая (линия) представляет собой (в данной системе координат) геометрическое место точек, координаты которых удовлетворяют уравнению (1)(И, П, стр. 95).

Иногда уравнение линии L представляют в параметрическом виде (2) при помощи третьей вспомогательной переменной (или параметра t) (И, П, стр.95):

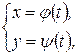(2)

где функци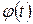и и 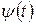предполагаются непрерывными по параметру t в некоторой области изменения параметра t. Иcключение параметра t из уравнений (2) в этом случае приводит приводит к уравнению (1).

Вид уравнения линии зависит как от самой линии, так и от выбранной системы координат.

При изучении линий, как правило, рассматриваются задачи двух типов (И, П, стр. 99):

1) изучение свойств линии при помощи заранее заданного уравнения этой линии, т.е. изучение геометрических свойств графика;

2) вывод уравнения линии, заранее заданной геометрически (как геометрическое место точек, удовлетворяющих некоторым условиям).

Плоские линии относительно декартовых прямоугольных координат подразделяют на алгебраические и неалгебраические (И, П, стр. 99)

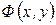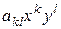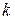Определение 1. Линия L называется алгебраической, если в некоторой декартовой прямоугольной системе координат он определяется уравнением (1), где представляет собой алгебраический полином, т.е. сумму конечного числа слагаемых вида , где и 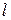- неотрицательные числа, а 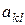- некоторые постоянные (И, П, стр. 99).

Определение 2. Всякая неалгебраическая линия называется трансцендентной (И, П, стр. 99).

Определение 3. Алгебраическая линия называется линией порядка n, если в которой декартовой прямоугольной системе координат эта линия определяется уравнением (1), в котором функция 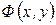представляет собой алгебраический полином n -ой степени (И, П, стр. 99).

Теорема 1. Если линия в некоторой декартовой прямоугольной системе координат определяется алгебраическим уравнением степени n, то эта линия и в любой другой декартовой системе координат определяется алгебраическим уравнением той же степени.

Доказательство (И., П., стр. 100, изучаете самостоятельно).