Каноническое уравнение параболы

Определение 21. Параболой называется геометрическое место точек плоскости, для которых расстояние до некоторой фиксированной точки F этой плоскости равно расстоянию до некоторой фиксированной прямой l, также расположенной в этой плоскости (И, П, стр. 147).

На рисунке 10 (https://desyatbukv.blogspot.ru/2012/01/blog-post_13.html) представлена кривая, удовлетворяющая данному определению.

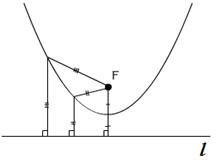
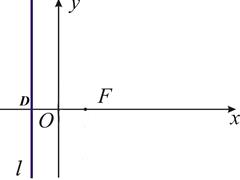
Рисунок 10 – Парабола Рисунок 11 – Каноническая система координат

Определение 22. Указанная в определении точка F называется фокусом параболы, а фиксированная прямая l – директрисой параболы (И, П, стр. 147).

Определение 23. Прямая, проходящая через фокус F параболы, перпендикулярно директрисе l параболы, называется её фокальной осью (или просто осью) (А, стр. 71).

Так как в случае, если 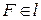, точки, для которых выполняются условия определения 21, принадлежат прямой, проходящей через F перпендикулярно l, т.е. парабола вырождается в прямую (И, П, стр. 147), в дальнейшем будет предполагать, что .

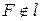Для вывода канонического уравнения параболы систему координат введем следующим образом (А, стр. 71; И, П, стр. 147). Обозначим точку пересечения фокальной оси и директрисы точкой D (рисунок). Начало О декартовой системы координат выберем в середине отрезка 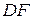, ось Ох сделаем сонаправленной вектору (рисунок 11).

Пусть длина отрезка DF равна р, . Тогда в выбранной системе координат точка F имеет координаты: , а прямая l, задается уравнением: . Пусть - произвольная точка плоскости. Обозначим через r расстояние от точки М до F, а через d – расстояние от точки М до директрисы l (рисунок 12, https://mixeraal.narod.ru/html/ur03.html).

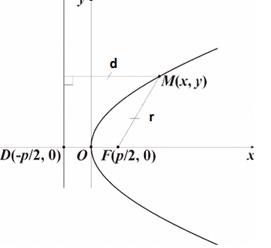
Рисунок 12

Точка М будет принадлежать указанному в определение 21 геометрическому множеству точек (параболе) тогда и только тогда, когда

. (37)

Поскольку для точек с отрицательными абсциссами всегда выполняется соотношение 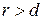(И, П, стр. 148), далее рассматриваем только точки с неотрицательными абсциссами.

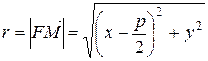; (38)

. (39)

Равенство (38) выполняется тогда и только тогда, когда

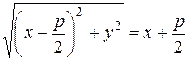. (40)

Возводя обе части уравнения (40) в квадрат и выполняя простейшие преобразования, получаем уравнение (41):

,

,

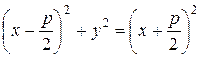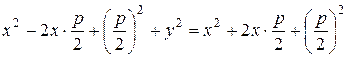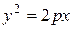. (41)

Так как уравнение (41) является следствием уравнения (40) необходимо проверить, все ли точки , координаты которых удовлетворяют уравнению (41) принадлежат параболе, т.е. для них выполняется свойство (37).

Пусть - точка плоскости, координаты которой удовлетворяют уравнению (41), тогда из (41) автоматически следует, что 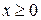и, значит, расстояние d от точки M до директрисы l определяется по правилу (39): .

Для определения расстояния r от точки М для фокуса F, воспользуемся формулой (38) и уравнением (41):

Так как, по доказанному выше, 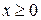, а, по постановке задачи, , то , и, следовательно, для всех точек , координаты которых удовлетворяют уравнению (41). Таким образом, условие (37) выполняется и точки принадлежат параболе.

Определение 24. Уравнение (41) называется каноническим уравнением параболы (И, П, стр. 148).

Определение 25. Расстояние р между фокусом и директрисой параболы называется фокальным параметром или просто параметром параболы (А, стр. 71).

Из уравнения (41) легко вывести следующие свойства параболы (А, стр. 71 – 72, И.П., стр. 154), отраженные на рисунке 13 (https://mixeraal.narod.ru/html/ur03.html):

1) Вся парабола расположена в правой полуплоскости;

2) фокальная ось является осью симметрии параболы;

3) парабола пересекается осями координат в точке О (0; 0), которая называется вершиной параболы и совпадает с началом системы координат, являющейся канонической для этой параболы.

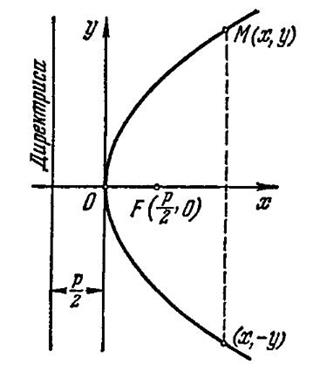
Рисунок 13 – Вид уравнения параболы в канонической системе координат

В заключение отметим, что для эллипса и гиперболы также можно определить директрисы (отдельно для каждого из фокусов). Подробнее об этом можно прочитать в учебниках Александров П.С. Курс аналитической геометрии и линейной алгебры (по изданию М: Наука, 1979, стр. 80 – 84) или Ильин В.А., Поздняк ЭГ. Аналитическая геометрия (по изданию М: Наука, 1988, стр. 155 -166). Там же можно ознакомиться с другими интересными свойствами рассмотренных кривых.