
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Линии первого порядка
|
|
Из школьного курса Вам известно, что любая прямая линия на плоскости (при фиксированной декартовой прямоугольной системе координат) определяется уравнением первой степени. Более того, имеет место теорема.
Теорема 2. Если на плоскости зафиксирована декартова прямоугольная система координат Оху, то любое уравнение вида (3):
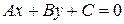 ,
, 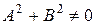 (3)
(3)
задает прямую на плоскости.
Доказательство (И, П, стр. 110-111).
Уравнение (3) называется общим уравнением прямой.
С другими способами задания прямой и способами определения взаимного расположения прямых по коэффициентам их уравнений можно ознакомиться по книге Ильин В.А., Поздняк Э.Г. Аналитическая геометрия, М.: Наука, 1988, стр. 110 – 126.
Мы же остановимся более подробно на изучении и способах задания алгебраических линий (кривых) второго порядка.
Наибольшее применение в приложениях имеют окружность, эллипс, гипербола и парабола. Свойства окружности Вам хорошо известны из школьного курса, поэтому мы на них не останавливаемся, а приступим к изучению свойств эллипса, гиперболы и параболы. В процессе которого покажем. Что окружность можно рассматривать. Как частный случай эллипса.