Переходные процессы в цепях с распределенными параметрами

Различают два типа задач, связанных с исследованием переходных процессов в одномерных цепях с распределенными параметрами:

1) определение токов и напряжений на зажимах линии при произвольном внешнем воздействии;

2) нахождение напряжений и токов в различных сечениях линии при произвольном внешнем воздействии.

Исследуем напряжение на выходе линии без потерь при согласованной нагрузке и введем понятие о линиях без искажений

Пусть при t < 0 напряжение на входе однородной линии без потерь u ₁ = 0, а при 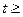0 оно изменяется по произвольному закону u ₁(t):

Найдем напряжение на выходе линии u ₂ для случая, когда сопротивление нагрузки линии равно волновому сопротивлению R _в.

Операторные изображения напряжений на входе U ₁ (р) и выходе U ₂ (р) линии связаны соотношением

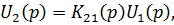
где K ₂₁ (р) — операторный коэффициент передачи линии по напряжению при согласованной нагрузке. Рассматривая линию как симметричный пассивный проходной четырехполюсник, получаем

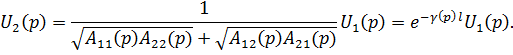
Для линии без потерь 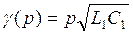поэтому .

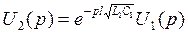Согласно теореме запаздывания (6.54), умножению изображения произвольной функции времени на 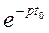соответствует смещение функции времени на t ₀ вправо. Следовательно,

Время запаздывания равно времени распространения падающей волны вдоль линии:

Таким образом, напряжение u ₂ на выходе линии без потерь при согласованной нагрузке представляет собой смещенное во времени на t₀ напряжение u ₁ на входе линии. Ток 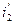на выходе линии повторяет по форме выходное напряжение u ₂ и равен смещенному во времени на t ₀ току на входе линии:

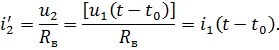
Следовательно, линия без потерь, работающая на согласованную нагрузку, осуществляет неискажающую передачу колебаний с входа линии на выход с задержкой на время, требуемое для распространения падающей волны вдоль линии.

Это свойство линии без потерь обусловлено тем, что фазовая скорость, волновое сопротивление и коэффициент ослабления линии без потерь не зависят от частоты. Если сложное воздействие на входе такой линии представить в виде суммы гармонических колебаний различных частот, то условия распространения колебаний всех частот будут одинаковы. Поэтому суммы гармонических колебаний на входе и выходе линии также одинаковы.

Можно убедиться, что условия неискажающей передачи выполняются и в линии с потерями, погонные параметры которой удовлетворяют условию

Комплексные волновое сопротивление и коэффициент распространения такой линии

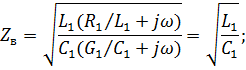
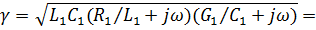
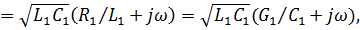
причем волновое сопротивление линии, фазовая скорость и коэффициент ослабления не зависят от частоты:

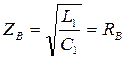
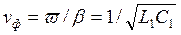
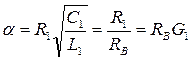
Если к входу линии, параметры которой удовлетворяют условию 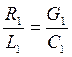, приложено произвольное напряжение u₁ = u₁(t) 1(t), то напряжение на выходе линии

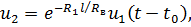
с ослаблением в 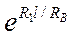раз и задержкой на t ₀ повторяет напряжение на ее входе.

Линии без потерь, а также линии, погонные параметры которых удовлетворяют условию 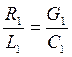, называются линиями без искажений. Рассмотренные свойства линий без искажения используются на практике для построения устройств задержки сигналов (линий задержки), назначение которых сдвигать сигнал во времени без искажения.