Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Коэффициент отражения линии. Определение постоянных интегрирования
|
|
Распределение токов и напряжений в длинной линии определяется не только волновыми параметрами, которые характеризуют собственные свойства линии и не зависят от свойств внешних по отношению к линии участков цепи, но и коэффициентом отражения линии, который зависит от степени согласования линии с нагрузкой.
Комплексным коэффициентом отражения длинной линии называется отношение комплексных действующих значений напряжений или токов отраженной и падающей волн в произвольном сечении линии:
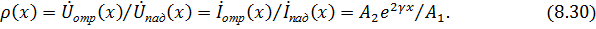
Для определения ρ (x) необходимо найти постоянные интегрирования А 1 и А 2, которые могут быть выражены через токи и напряжения в начале (x = 0) или конце (x = l) линии. Пусть в конце линии (см. рис.3) напряжение линии u2 = u(l, t) = u(x, t)|x=l, а ее ток i2 = i(l, t) = i(x, t)|x=l.
Обозначая комплексные действующие значения этих величин через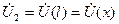 
)|x=l => u2 и 
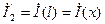)|x=l => 
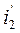и полагая в (8.10), (8.11) x = l получаем
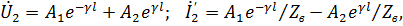
откуда
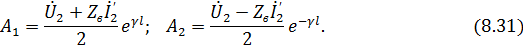
Подставляя (8.31) в (8.30), выражаем коэффициент отражения через ток и напряжение в конце линии:
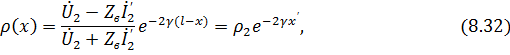
где x’ = l – x — расстояние, отсчитываемое от конца линии;
ρ 2 = ρ (x)|x=l =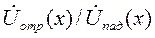 
)|x=l = 
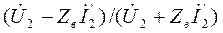— коэффициент отражения в конце линии, значение которого определяется только соотношением между сопротивлением нагрузки 
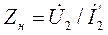и волновым сопротивлением линии Z в:
Как и всякое комплексное число, коэффициент отражения линии может быть представлен в показательной форме:
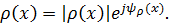
Анализируя выражение (8.32), устанавливаем, что модуль коэффициента отражения
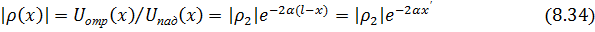
плавно увеличивается с ростом x и достигает наибольшего значения ρ max(x) = ρ 2 в конце линии.
Выражая коэффициент отражения в начале линии ρ 1 через коэффициент отражения в конце линии ρ 2
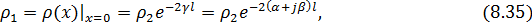
находим, что модуль коэффициента отражения в начале линии в e2 α l раз меньше, чем модуль коэффициента отражения в ее конце. Из выражений (8.34), (8.35) следует, что модуль коэффициента отражения однородной линии без потерь имеет одно и то же значение во всех сечениях линии.
С помощью формул (8.31), (8.33) напряжение и ток в произвольном сечении линии можно выразить через напряжение или ток и коэффициент отражения в конце линии:
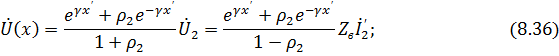
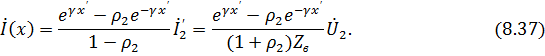
Выражения (8.36) и (8.37) позволяют рассмотреть распределение напряжений и токов в однородной длинной линии в некоторых характерных режимах ее работы.