Общее решение дифференциальных уравнений длинной линии

Задача анализа цепей с распределенными параметрами обычно сводится к определению законов изменения токов и напряжений вдоль цепи, а также к исследованию частотных или временных характеристик цепи относительно внешних зажимов. С этой целью необходимо найти частные решения дифференциальных уравнений линии (1.44), (1.45) при соответствующих начальных и граничных условиях. Мы ограничимся рассмотрением однородной линии длиной l (рис.3), поскольку решение данных уравнений для неоднородных линий может быть получено только при некоторых частных видах зависимостей погонных параметров от координаты.

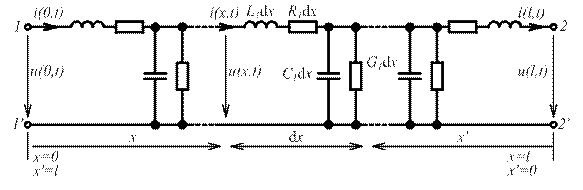
Рис.3. Схема замещения однородной длинной линии

Для решения дифференциальных уравнений линии используют операторный метод, который позволяет перейти от решения дифференциальных уравнений в частных производных для мгновенных значений токов 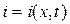и напряжений 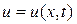линии к решению обыкновенных дифференциальных уравнений, составленных относительно операторных изображений соответствующих токов 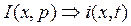и напряжений .

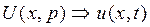В курсе ОТЦ показано, что при нулевых начальных условиях, т.е. при и 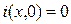, задача сводится к решению двух дифференциальных уравнений:

уравнения, составленного относительно напряжения:

и уравнения, связывающего напряжение и ток:

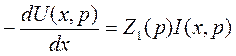
Входящие в эти уравнения величины

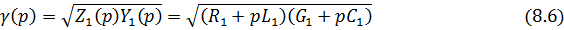
называется операторным коэффициентом распространения, а параметры

Z ₁(p) = R ₁ + pL ₁, Y ₁(p) = G ₁ + pC ₁

называется операторным погонным сопротивлением и погонной проводимостью линии.

Таким образом, распределение операторных изображений токов и напряжений в линейной однородной инвариантной во времени цепи с распределенными параметрами описывается решениями линейного дифференциального уравнения второго порядка с постоянными коэффициентами, общее решение которого имеет вид

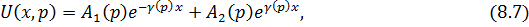
где А ₁(р), А ₂(р) — постоянные интегрирования, определяемые граничными условиями задачи, т.е. значениями неизвестных функци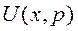й и 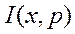в начале (x = 0) или в конце (x = l) линии.

Выражение для операторного изображения тока линии

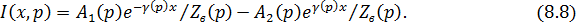
где величина

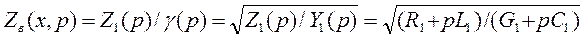
называется операторным волновым сопротивлением линии.

Определяя значения постоянных интегрирования А ₁(р), А ₂(р), соответствующие тем или иным граничным условиям, и подставляя их в выражения для и , можно получить операторные изображения тока и напряжения в любом сечении линии при произвольном внешнем воздействии, а также найти любые частотные и временные характеристики исследуемой цепи.