Задача анализа цепей с распределенными параметрами

Основные отличия цепей с сосредоточенными параметрами от цепей с распределенными параметрами состоят в следующем.

Электрические цепи, процессы в которых описываются обыкновенными дифференциальными уравнениями, называются цепями с сосредоточенными параметрами. Цепи такого типа используют на сравнительно низких частотах, когда длина волны электромагнитных колебаний существенно больше размеров исследуемого устройства.

При этих условиях в исследуемых устройствах и их элементах удается выделить конечное число участков, в которых преобладает какой-то один из основных эффектов — запасание энергии электрического или магнитного полей, преобразование электрической энергии в другие виды энергии или преобразование энергии сторонних сил в электрическую. Токи рассматриваемой реальной цепи, являясь функциями времени, имеют одинаковые мгновенные значения в пределах каждого из выделенных участков. Заменяя эти участки идеализированными активными или пассивными элементами, получают идеализированную цепь, содержащую конечное число элементов, значения параметров которых конечны.

Таким образом, цепи с сосредоточенными параметрами представляют собой идеализированные цепи, моделирующие реальные устройства или их элементы при условиях, когда можно предположить, что каждый из перечисленных выше основных электрических эффектов проявляется в конечном числе пространственно локализуемых областей.

Направляющие системы используются в электросвязи для передачи сообщений на большие расстояния при высокой частоте и скорости передаваемого сообщения. Очевидно, что направляющие системы имеют больш у ю протяженность, и поэтому длина линии связи соизмерима или существенно больше длины волны используемых электромагнитных колебаний.

В этих условиях невозможно пространственно локализовать области, в которых проявляются только эффекты одного типа. Это связано с тем, что даже при бесконечно малой длине выделяемых участков, в пределах каждого из них одновременно имеют место несколько из перечисленных основных эффектов, причем ток в пределах выделенных участков изменяется от одного сечения к другому. При этом цепи, моделирующие реальные устройства, должны содержать бесконечно большое число идеализированных элементов, параметры которых имеют бесконечно малые значения. Процессы в таких цепях описываются дифференциальными уравнениями в частных производных, а цепи называются цепями с распределенными параметрами.

В зависимости от условий и требуемой точности исследования каждый элемент реальной цепи и, следовательно, каждая реальная цепь в целом могут быть заменены моделирующей цепью с сосредоточенными или распределенными параметрами.

Рассмотрим, например, конденсатор, который конструктивно представляет собой две проводящие обкладки 1 и 3, разделенные слоем диэлектрика 2 (рис. 1.41).

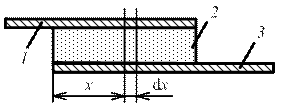
Рис.1. Упрощенная конструкция конденсатора

На частотах до 1ГГц (λ > 30см), когда длина волны электромагнитных колебаний значительно превышает геометрические размеры обкладок, он может быть представлен одной из моделирующих цепей с сосредоточенными параметрами. На более высоких частотах, когда длина волны электромагнитных колебаний сравнима с геометрическими размерами обкладок, необходимо учитывать, что процессы запасания энергии электрического и магнитного полей, а также необратимое преобразование электрической энергии в другие виды энергии имеют место вдоль всей длины обкладок конденсатора. В этом случае схема замещения элементарного участка конденсатора длиной d x будет содержать индуктивность L ₀ и емкость С ₀, характеризующие процессы запасания энергии магнитного и электрического полей, а также сопротивление R ₀ и проводимость утечки G ₀, учитывающие потери энергии в конденсаторе (рис.2, а). Схема замещения всего конденсатора должна состоять из бесконечно большого числа таких секций. Следовательно, идеализированная цепь, моделирующая конденсатор в рассматриваемом диапазоне частот, представляет собой цепь с распределенными параметрами.

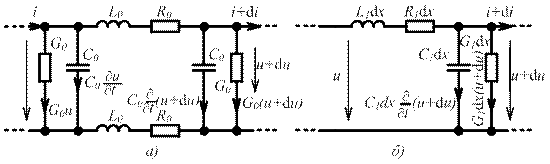
Рис.2. К определению понятия цепи с распределенными параметрами

На примере цепи, схема которой изображена на рис.2, а, можно показать, что электрические процессы в цепях с распределенными параметрами описываются дифференциальными уравнениями в частных производных. Действительно, ток i = i(x, t) и напряжение u = u(х, t) рассматриваемой цепи являются функциями времени t и координаты х. Приращения тока и напряжения на участке цепи длиной d x

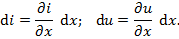
Будем считать, что параметры элементов моделирующей цепи R ₀, L ₀, С ₀ и G ₀ не зависят от токов и напряжений, и их можно выразить через погонные (т. е. приходящиеся на единицу длины) параметры R ₁, L ₁, С ₁ и G ₁:

R ₀ = (R ₁ /2)d x; L ₀ = (L ₁ /2)d x; C ₀= (C ₁ /2)dx; G ₀ = (G ₁ /2)d x.

На основе уравнения баланса токов и напряжений элементарного участка цепи (рис.2, а) могут быть получены следующие соотношения:

Решая уравнения (1.44), (1.45) при соответствующих начальных и граничных условиях, можно определить токи и напряжения цепи с распределенными параметрами в конкретном режиме.

Отметим, что уравнениям (1.44), (1.45) может быть поставлена в соответствие более простая схема замещения элементарного участка цепи (рис.2, б). Аналогичный вид имеют высокочастотные схемы замещения и ряда других элементов, входящих в состав радиоэлектронных устройств, в частности двухпроводных и коаксиальных линий передачи.

В зависимости от числа координат, вдоль которых происходит изменение тока и напряжения и вдоль которых «распределены» параметры цепи, различают одномерные, двухмерные и трехмерные цепи с распределенными параметрами. В курсе «Направляющие системы электросвязи» нас будут интересовать в основном одномерные цепи с распределенными параметрами, процессы в которых описываются дифференциальными уравнениями (1.44), (1.45).

Итак, токи и напряжения в одномерной цепи с распределенными параметрами являются функциями двух переменных — времени t и координаты x.

Исторически сложилось так, что первыми в качестве одномерных цепей с распределенными параметрами стали представлять так называемые длинные линии, т. е. линии передачи энергии от источника к нагрузке, длина которых значительно превышает длину волны передаваемых электромагнитных колебаний. Поэтому одномерные цепи с распределенными параметрами часто называют длинными линиями или линиями, а уравнения (1.44), (1.45), описывающие зависимости между токами и напряжениями элементарного участка одномерной цепи с распределенными параметрами, — дифференциальными уравнениями длинной линии или телеграфными уравнениями. Мы будем использовать термины «длинная линия» или «линия» как синонимы термина «одномерная цепь с распределенными параметрами».

Одномерные цепи с распределенными параметрами, применяемые для моделирования различных реальных цепей и их элементов, отличаются одна от другой в основном значениями погонных параметров R ₁, L ₁, С ₁, G ₁ и характером их зависимости от координаты, времени или режима работы цепи. В линейных инвариантных во времени цепях с распределенными параметрами погонное сопротивление R ₁, индуктивность L ₁, емкость С ₁ и проводимость утечки G ₁ не зависят от времени и режима работы цепи. Погонные параметры могут изменяться вдоль цепи по определенному закону либо иметь одинаковые значения на всех ее участках. Линейные инвариантные во времени цепи с распределенными параметрами, погонные параметры которых постоянны и не зависят от координаты, называются однородными (регулярными). Цепи, погонные параметры которых являются функциями координаты, называются неоднородными (нерегулярными).

В зависимости от того, какие процессы в исследуемой реальной цепи имеют преобладающий характер, а также от степени идеализации схема замещения элементарного участка линии может не содержать тех или иных из показанных на рис.2 элементов. В соответствии с этим цепи с распределенными параметрами подразделяют на цепи без потерь (LC -линии), индуктивно-емкостные с потерями (LCR -линии), резистивно-емкостные (RС -линии), резистивно-индуктивные (RL -линии) и резистивные (RG -линии). Нас будут в большей степени интересовать процессы в линиях без потерь и в линиях общего вида с малыми потерями, которые используются в основном для моделирования реальных линий передачи в современной телефонии.