
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Основы математической статистики
|
|
Статистические методы обработки результатов исследования: представление и интерпретация
Формы представления эмпирических данных
Данные в статистике – это основные элементы, подлежащие анализу. Данными могут быть какие-то количественные результаты, свойства, присущие определенным элементам генеральной совокупности, место в той или иной последовательности, то есть любая информация, которая может быть классифицирована по категориям с целью обработки.
Не следует смешивать «данные» с теми «значениями», которые эти данные могут принимать. Для того чтобы всегда различать их, следует запомнить, что данные часто принимают одни и те же значения. Например, если взять 10 данных по числу выполненных заданий теста: 22, 25, 20, 27, 29, 27, 27, 28, 25, 29, то они принимают только 6 разных значений: 20, 22, 25, 27, 28, 29.
На языке математики отдельные числовые значения варьирующего параметра называют вариантами. Все изучаемые показатели признака варьируются, но не все поддаются непосредственному измерению.
Существует три типа данных:
1. Количественные данные, допускающие непосредственное измерение величины признака. Их можно распределить по числовой шкале с равными интервалами. Количественные данные могут быть непрерывными и дискретными. Непрерывные данные могут принимать любое значение на непрерывной шкале (данные о весе, размерах, времени и т.д.). У непрерывных данных значения никогда не могут быть зафиксированы точно, поэтому его округляют до ближайшего значения. Дискретные данные могут принимать лишь определенные значения из диапазона измерений (результаты тестирования, экзаменационные оценки и т.п.). Дискретная величина принимает конечное или бесконечное счетное множество значений, которые могут быть занумерованы в каком-либо порядке и выписаны в последовательность.
2. Качественные данные, представляющие собой какие-то свойства элементов выборки или популяции (пол, национальность, тип темперамента и пр.). Их нельзя измерить, и единственной их количественной оценкой служит частота встречаемости (число лиц с сильной и слабой нервной системой и т.п.).
3. Порядковые данные занимают промежуточное положение между количественными и качественными типами данных. Порядковые данные соответствуют местам элементов в последовательности, полученной при их расположении в возрастающем порядке (1-й, 2-й, …n-й, …; А, В, С, …). Их можно упорядочить как количественные данные, но над ними нельзя производить арифметические действия, как и над качественными данными.
Основы математической статистики
Математическая статистика – это наука о случайных явлениях. Под статистикой понимают науку, изучающую методы сбора и интерпретации числовых данных, то есть методы, служащие для принятия обоснованных решений в условиях неопределенности. Цель статистики – синтез данных, полученных на различных группах объектов в том или ином эксперименте, в их сравнении с целью выявить черты различия между ними, в их сопоставлении с целью выявить показатели, измеряющиеся в одном направлении, в предсказании определенных фактов на основании тех выводов, к которым приводят полученные результаты и т.д.
Выделяют три главных раздела статистики:
1. Описательная статистика рассматривает вопросы описания картины случайного распределения по данным наблюдений массовых явлений. Она позволяет описывать, подытоживать, воспроизводить в виде таблиц или графиков данные того или иного распределения, вычислять среднее для данного распределения, его размах, дисперсию и др.
2. Индуктивная статистика занимается статистической проверкой гипотез, т.е. проверкой того, можно ли распространить результаты, полученные на данной выборке, на всю популяцию, из которой взята выборка. Правила этого раздела статистики позволяют выяснить, до какой степени можно путем индукции обобщить на большее число объектов ту или иную закономерность, обнаруженную при изучении их ограниченной группы в ходе какого-либо наблюдения или эксперимента.
3. Теория корреляции – учение о зависимости между величинами, о связи между величинами, каждая из которых испытывает вариации под действием случайных факторов. Измерение корреляции позволяет узнать, насколько связаны между собой две переменные, с тем, чтобы можно было предсказывать возможные значения одной из них, если известна другая.
Существует два вида статистических методов, позволяющих делать обобщение или вычислять степень корреляции:
а) Параметрические методы, в которых используются такие параметры, как среднее значение или дисперсия данных. Для использования параметрических методов необходимы три условия: данные должны быть количественными, их число должно быть достаточным, а распределение – нормальным;
б) Непараметрические методы, когда исследователь имеет дело с очень малыми выборками или с качественными или порядковыми данными. Непараметрические методы рекомендуется использовать во всех остальных случаях.
Распределением признака называется закономерность встречаемости разных его значений. Параметры распределения – это его числовые характеристики, указывающие, где «в среднем» располагаются значения признака, насколько эти значения изменчивы и наблюдается ли преимущественное появление определенных значений признака. В реальных психолого-педагогических исследованиях мы оперируем не параметрами, а их приближенными значениями, так называемыми оценками параметров. Это объясняется ограниченностью обследованных выборок. Чем больше выборка, тем ближе может быть оценка параметра к его истинному значению. В дальнейшем, говоря о параметрах, мы будем иметь в виду их оценки.
Производя наблюдения над каким-либо признаком совокупности объектов или опытов, на практике получаем эмпирические распределения непрерывной величины, количественное выражение которого в некоторых единицах может в принципе непрерывно изменяться. Тот факт, что измеряемая величина принимает определенное числовое значение, можно рассматривать как случайное событие и охарактеризовать возможность его появления вероятностью, частотой или частостью.
Частотой события называется количество случаев появления событий. Частота зависит от количества испытаний. В качестве сравнительной оценки возможности появления случайных событий частота может служить лишь при условии одинакового числа испытаний. Если же это условие не выполняется, то нужна другая мера. Такой мерой возможности появления случайных событий является частость. Частость – это относительная частота, т.е. частота, деленная на количество испытаний. Она в гораздо меньшей степени зависит от количества испытаний, чем частота. Обозначая частоту f, количество испытаний n, а частость p, можем записать: p=f / n.
Рассмотрим пример: Ниже представлено число правильных ответов по какому-либо тесту пятнадцати испытуемых.
23, 25, 24, 27, 25, 32, 27, 29, 22, 20, 24, 25, 27, 28, 29 (n=15).
Число правильных ответов является варьирующим признаком, поэтому расположим данные в порядке возрастания:
20, 22, 23, 24, 24, 25, 25, 25, 27, 27, 27, 28, 29, 29, 32 (n=15).
 В таком расположении рассматриваемые данные представляют вариационный ряд, т.е. ряд данных, расположенных в порядке возрастания варьирующего признака. Промежуток между крайними членами вариационного ряда называют интервалом варьирования, а длину этого интервала – размахом.
В таком расположении рассматриваемые данные представляют вариационный ряд, т.е. ряд данных, расположенных в порядке возрастания варьирующего признака. Промежуток между крайними членами вариационного ряда называют интервалом варьирования, а длину этого интервала – размахом.
Сразу можно отметить, что некоторые данные принимают одни и те же значения, причем одни значения встречаются чаще, а другие – реже. Представим распределение значений с учетом их частот графически (получаются столбиковые диаграммы):

* *
* * * *
* * * * * * * * *
| 20 21 22 23 24 25 26 27 28 29 30 31 32 33 |
Такое распределение данных по их значениям дает нам уже гораздо больше, чем представление в виде рядов. Однако подобную группировку используют в основном лишь для качественных данных, четко разделяющихся на обособленные категории. Что касается количественных данных, то они всегда многочисленны. Поэтому такие данные предпочитают группировать по классам, чтобы яснее была видна основная тенденция распределения.
Такая группировка состоит в основном в том, что данные с одинаковыми или близкими значениями объединяют в классы и определяют частоту для каждого класса. Способ разбиения на классы зависит от того, что именно экспериментатор хочет выявить при разделении измерительной шкалы на равные интервалы. Однако очевидно, что когда данные расположены по классам, то некоторая часть информации теряется. Если затем попытаться оценить среднее значение и дисперсию, группированных данных, то получатся приближенные данные (с потерей точности).
В нашем случае можно сгруппировать данные по классам с интервалами в три единицы шкалы:
| Классы | 19-21 | 22-24 | 25-27 | 28-30 | 31-33 |
| Частоты |
Данные, разбитые на классы по непрерывной шкале, нельзя представить графически так, как мы только что рассмотрели, поэтому предпочитают использовать:
гистограммы - способ графического представления в виде примыкающих друг к другу прямоугольников;
полигоны распределения частот, когда отрезками прямых соединяют центры верхних сторон всех прямоугольников гистограммы, а затем с обеих сторон «замыкают» площадь под кривой, доводя концы полигонов до горизонтальной оси (частота = 0) в точках, соответствующих самым крайним значениям распределения;
кумуляты – когда на оси абсцисс наносят срединные значения классов, а по оси ординат – накопленные частоты классов.
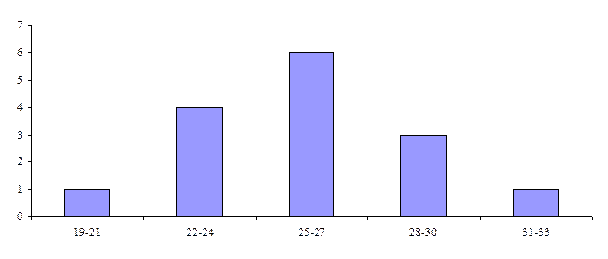
Гистограмма распределения исходных данных
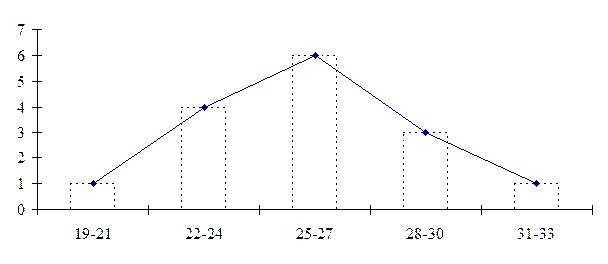
Полигон распределения исходных данных
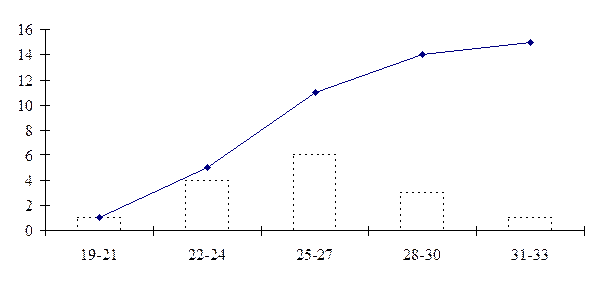
Кумулята распределения исходных данных