T – критерий Стьюдента

Это параметрический метод, используемый для проверки гипотез о достоверности разницы средних при анализе количественных данных в популяциях с нормальным распределением и с одинаковой дисперсией. Он хорошо применим в случае сравнения величин средних случайных значений измеряемого признака в контрольной и экспериментальной группах, в различных половозрастных группах, группах, имеющих другие различные признаки.

Обязательным условием применимости параметрических методов, в том числе и t‑ критерия Стьюдента, для доказательства статистических гипотез является подчинение эмпирического распределения исследуемого признака закону нормального распределения.

Метод Стьюдента различен для независимых и зависимых выборок.

Независимые выборки получаются при исследовании двух различных групп испытуемых (например, контрольной и опытной групп). К зависимым выборкам относятся, например, результаты одной и той же группы испытуемых до и после воздействия независимой переменной.

Проверяемая гипотеза Н₀ состоит в том, что разность между средними значениями двух выборок равна нулю ( 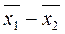= 0), другими словами это гипотеза о равенстве средних ( 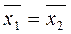). Альтернативная гипотеза Н₁ состоит в том, что эта разность отлична от нуля ( 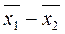¹ 0) или же существует отличие выборочных средних ( ).

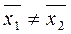В случае независимых выборок для анализа разницы средних применяют формулу: 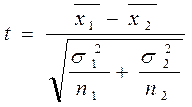при n₁, n₂ > 30

и формулу 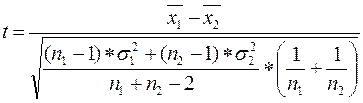при n₁, n₂ < 30, где

- среднее арифметическое значение первой выборки;

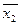- среднее арифметической значение второй выборки;

s₁ – стандартное отклонение для первой выборки;

s₂ – стандартное отклонение для второй выборки;

n₁ и n₂ – число элементов в первой и второй выборках.

Для нахождения критического значения t определим число степеней свободы:

n = n₁ - 1 + n₂ - 1 = (n₁ + n₂) – 2 = n - 2.

Если |t_эмп | > t_кр, то нулевую гипотезу отбрасываем и принимаем альтернативную, то есть считаем разницу средних достоверной. Если |t_эмп | < t_кр, то разница средних недостоверна.

В случае зависимых выборок для определения достоверности разницы средних применяется следующая формула: , где

d – разность между результатами в каждой паре (х_i – y_i);

å d – сумма этих частных разностей;

å d² – сумма квадратов частных разностей;

n – число пар данных.

Число степеней свободы в случае зависимых выборок для определения t критерия будет равно n = n - 1.

Существуют и другие статистические критерии проверки гипотез, как параметрические, так и непараметрические. Например, математико-статистический критерий, позволяющий судить о сходстве и различиях в дисперсиях случайных величин, называется критерием Фишера.