
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Меры рассеяния статистических совокупностей
|
|
Для количественной оценки разброса результатов относительно среднего в том или ином распределении существуют точные методы. Чаще всего для оценки разброса определяют отклонение каждого из полученных значений от среднего d = 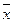 - xi. Затем вычисляют среднее арифметическое всех этих отклонений:
- xi. Затем вычисляют среднее арифметическое всех этих отклонений: 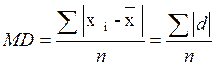 . Чем больше среднее отклонение, тем больше разброс данных и тем более разнородна выборка.
. Чем больше среднее отклонение, тем больше разброс данных и тем более разнородна выборка.
Однако в алгебраических формулах, используемых в более сложном статистическом анализе, оперировать абсолютными значениями довольно трудно. Поэтому, чтобы не использовать значения с отрицательным знаком, математики сначала возводят все значения в квадрат, а затем делят сумму квадратов на число данных. В результате такого расчета получают дисперсию: s 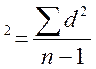 .
.
Сам термин «дисперсия» означает «рассеивание». Это параметр, отвечающий за «распластанность» графика плотности вероятности вдоль оси Х. Однако там, где требуется учитывать качество (наименование) случайной величины, квадратическая мера, какой является дисперсия, неудобна и тогда применяется стандартное отклонение.
Стандартное отклонение определяется как положительное значение квадратного корня из дисперсии: s = 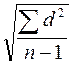 .
.
Дисперсия является показателем разброса экспериментальных данных, характеризует среднюю величину отклонения индивидуальных показателей от среднего значения по выборке. Т.е ., дисперсия показывает величину отклонения частных значений от средней величины в данной выборке. Дисперсия удобна для выявления влияния различных факторов на индивидуальное выполнение тестовых заданий, стандартное отклонение широко применяется как мера сравнения разбросов результатов измерений в различных группах.