
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Проверка статистических гипотез
|
|
Формулирование гипотез систематизирует предположения исследователя и представляет их в четком, лаконичном виде. Решение, которое требуется принять исследователю, касается истинности или ложности статистической гипотезы. Различают два вида гипотез: научные и статистические. Научная гипотеза – это предполагаемое решение проблемы (формулируется как теорема). Статистическая гипотеза – просто утверждение относительно неизвестного параметра генеральной совокупности (свойстве случайной величины или событии), которое формулируется для проверки надежности связи и которое можно проверить по известным выборочным статистикам (результатам исследования, имеющимся эмпирическим данным).
Статистические гипотезы подразделяются на нулевые и альтернативные, направленные и ненаправленные. Нулевая гипотеза (Н0) это гипотеза об отсутствии различий, отсутствие влияния фактора, отсутствие эффекта и т.п. Это то, что предполагается опровергнуть, если перед нами стоит задача доказать значимость различий. Альтернативная гипотеза (Н1) это гипотеза о значимости различий. Это то, что предполагается доказать, поэтому ее иногда называют экспериментальной или рабочей гипотезой.
Сама же процедура обработки полученных количественных данных, заключающаяся в вычислении некоторых статистических характеристик и оценок, позволяющих проверить нулевую гипотезу называется статистическим анализом.
Нулевая и альтернативная гипотезы могут быть направленными и ненаправленными. Гипотеза называется направленной, если она содержит указание на направление отличий. Такие гипотезы следует формулировать, например, в том случае, если в одной из групп индивидуальные значения испытуемых по какому-либо признаку выше, а в другой ниже, или необходимо доказать, что в одной из групп под влиянием каких-либо экспериментальных воздействий произошли более выраженные изменения, чем в другой группе. Гипотеза называется ненаправленной, если ее формулировка предполагает лишь определение отличий или не отличий (без указания направления отличий). Например, если необходимо доказать, в двух разных группах различаются формы распределения признака.
Примеры формулирования гипотез.
| Направленные гипотезы | Ненаправленные гипотезы |
| Н0: Х1 не превышает Х2 | Н0: Х1 не отличается от Х2 |
| Н1: Х1 превышает Х2 | Н1: Х1 отличается от Х2 |
Метод, который используется для принятия решения относительно справедливости статистической гипотезы, называется проверкой гипотезы. Основной принцип проверки гипотезы состоит в том, что выдвигается нулевая гипотеза Н0, с тем, чтобы попытаться опровергнуть ее и тем самым подтвердить альтернативную гипотезу Н1.
При проверке любой статистической гипотезы решение исследователя никогда не принимается с уверенностью, поскольку всегда остается риск принятия неправильного решения.
Обычно используемые выборки невелики, и в этих случаях вероятность ошибки может быть значительной. Существует так называемый уровень достоверности (уровень значимости) различия. Это вероятность того, что различия считаются существенными, а они на самом деле случайны. То есть это вероятность отклонения нулевой гипотезы, в то время как она верна.
Когда указывается, что различия достоверны на 5%-ном уровне значимости, или при p£ 0, 05, то имеется в виду, что вероятность того, что они все-таки недостоверны, составляет 0, 05 (низший уровень статистической значимости). Если указывается, что различия достоверны на 1%-ном уровне значимости, или при p£ 0, 01, то имеется в виду, что вероятность того, что они все-таки недостоверны, составляет 0, 01 (достаточный уровень статистической значимости). Если указывается, что различия достоверны на 0, 1%-ном уровне значимости, или при p£ 0, 001, то имеется в виду, что вероятность того, что они все-таки недостоверны, составляет 0, 001 (высший уровень статистической значимости).
Правило отклонения Н0 и принятия Н1 :
Если эмпирическое значение критерия равняется критическому значению, соответствующему p£ 0, 05 или превышает его, то Н0 отклоняется, но еще нельзя определенно принять Н1.
Если эмпирическое значение критерия равняется критическому значению, соответствующему p£ 0, 01 или превышает его, то Н0 отклоняется принимается Н1.
Для наглядности правила принятия решения можно использовать так называемую «ось значимости».
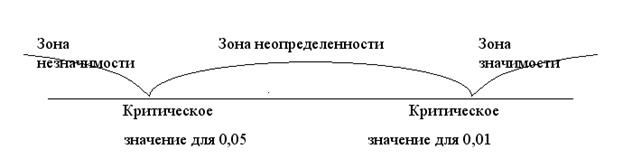
Если уровень достоверности не превышен, то можно считать вероятным, что выявленная разница действительно отражает положение дел в популяции. Для каждого статистического метода этот уровень можно узнать из таблиц распределения критических значений соответствующих критериев.